Suite récurrente, un peu tout
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction numérique
On considère la suite
- Déterminer le sens de variation de
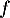 sur
sur 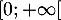 .
(Les limites aux bornes ne sont pas demandées)
.
(Les limites aux bornes ne sont pas demandées)
- Calculer
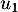 et
et 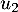 .
.
-
- Démontrer par récurrence que, pour tout entier naturel
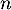 ,
on a:
,
on a: 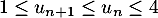 .
.
- En déduire que la suite
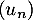 est convergente.
est convergente.
- On appelle
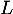 la limite de la suite
la limite de la suite 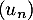 .
Déterminer la valeur de
.
Déterminer la valeur de 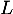 .
.
- Démontrer par récurrence que, pour tout entier naturel
-
- Recopier et compléter la fonction Python ci-dessous qui,
pour tout réel positif
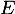 , détermine la plus petite valeur
, détermine la plus petite valeur 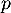 tel que
tel que
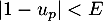 .
.
![\[\fbox{\begin{minipage}{6cm}
\texttt{def Seuil(E):}\\
\hspace*{1em}\texttt{u=4}\\
\hspace*{1em}\texttt{n=0}\\
\hspace*{1em}\texttt{while \ \dots}\\
\hspace*{2em}\texttt{u= \ \dots }\\
\hspace*{2em}\texttt{n=n+1}\\
\hspace*{1em}\texttt{return n}
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapSuites/exSR-cplt/21.png)
- Donner la valeur renvoyée par ce programme dans le cas où
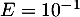 .
.
- Recopier et compléter la fonction Python ci-dessous qui,
pour tout réel positif
- On considère la suite
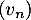 définie,
pour tout entier naturel
définie,
pour tout entier naturel 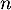 , par:
, par:
![\[v_n=\dfrac1{u_n-1}\]](/Generateur-Devoirs/TS/ChapSuites/exSR-cplt/25.png)
- Démontrer que la suite
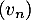 est arithmétique
dont vous donnerez le premier terme et la raison.
est arithmétique
dont vous donnerez le premier terme et la raison.
- En déduire, pour tout entier naturel
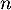 ,
l'expression de
,
l'expression de 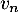 en fonction de
en fonction de 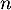 .
.
- Calculer la limite de la suite
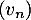 .
.
- Puis retrouver par le calcul la limite de la suite
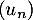 .
.
- Démontrer que la suite
Correction
Tag:Suites
Voir aussi:
Quelques devoirs
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, suite auxiliaire géométrique
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, construction géométrique des premiers termes d'une suite récurrente, convergence monotone et point fixe
maison sur les fonctions: calcus de dérivées et sens de variation, et les suites: démonstration par récurrence, suite auxiliaire arithmétique, convergence monotone et point fixe
