Suite récurrente et exponentielle
Exercice corrigé - Spécialité maths, terminale générale
Le but de cet exercice est d'étudier la suite 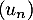 définie par:
définie par:
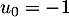 et, pour tout entier naturel
et, pour tout entier naturel 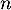 ,
,
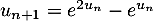 .
.
On remarquera que cette égalité peut aussi s'écrire: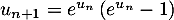 .
.
On pourra poser éventuellement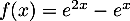 .
.
On remarquera que cette égalité peut aussi s'écrire:
On pourra poser éventuellement
- Soit
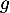 la fonction définie pour tout réel
la fonction définie pour tout réel 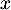 par
par
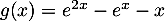 .
.
- Déterminer les limites de
 en
en  et
et  .
.
- Calculer
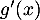 et prouver que, pour tout réel
et prouver que, pour tout réel 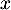 ,
,
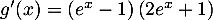 .
.
- Déterminer les variations de la fonction
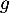 et donner la valeur de
son minimum.
et donner la valeur de
son minimum.
- Déterminer les limites de
-
- En remarquant que
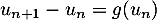 ,
étudier le sens de variation de la suite
,
étudier le sens de variation de la suite 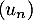 .
.
- Démontrer par récurrence que, pour tout entier
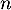 ,
,
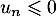 .
.
- Montrer que la suite
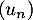 est convergente vers une limite
est convergente vers une limite 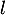 qui vérifie
qui vérifie 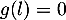 .
En déduire la limite
.
En déduire la limite 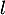 .
.
- En remarquant que
Correction
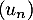 est définie par
est définie par 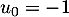 et, pour
et, pour 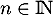 ,
,
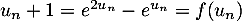 ,
avec
,
avec 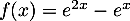 .
.
On a aussi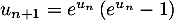 .
.
Cacher la correction
On a aussi
- Soit
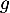 la fonction définie pour tout réel
la fonction définie pour tout réel 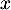 par
par
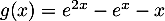 .
.
- En
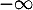 , on a
, on a
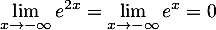 d'où
d'où
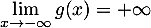 .
.
En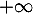 ,
,
![\[g(x)=e^{2x}\lp1-\dfrac{e^x}{e^{2x}}-\dfrac{x}{e^{2x}}\right)
=e^{2x}\lp1-\dfrac1{e^x}-\dfrac{x}{e^{2x}}\right)
\]](/Generateur-Devoirs/TS/ChapExponentielle/exSRexp_c/14.png)
avec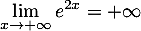 et
et 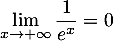 .
.
Enfin,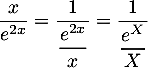 en posant
en posant 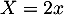 ,
et, comme par croissances comparées,
,
et, comme par croissances comparées,
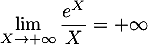 ,
on a
,
on a 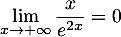 et donc
et donc
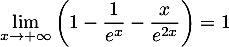 .
.
On trouve donc finalement, par produit des limites,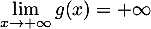 .
.
- On a
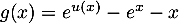 avec
avec 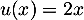 ,
et donc
,
et donc 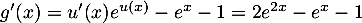 .
.
Par ailleurs, en développant l'expression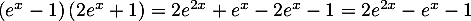
on obtient bien que, pour tout réel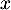 ,
,
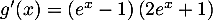 .
.
- Comme pour tout réel
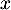 , on a
, on a 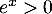 donc
donc 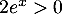 et
on a donc
et
on a donc 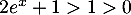 .
.
Par ailleurs,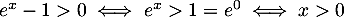 comme la fonction exponentielle est strictement croissante sur
comme la fonction exponentielle est strictement croissante sur 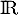 .
.
On peut alors dresser le tableau de signes:
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ &$-\infty$ && 0 && $+\infty$ \\\hline
$e^x-1$ && $-$ &0& $+$ &\\\hline
$2e^x+1$ && $+$ &$|$& $+$ &\\\hline
$g'(x)$ && $-$ &0& $+$ &\\\hline
&$+\infty$&&&&$+\infty$\\
$g$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&0&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/exSRexp_c/35.png)
On calcule aussi le minimum: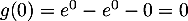 .
.
- En
-
- On vient de trouver à la question précédente,
que
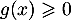 pour tout
pour tout 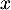 réel.
réel.
Ainsi,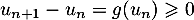 ,
ce qui montre que la suite
,
ce qui montre que la suite 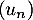 est croissante.
est croissante.
- Soit la proposition
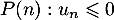 .
.
Initialisation: Pour , on a
, on a 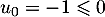 et donc
et donc 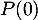 est vraie.
est vraie.
Hérédité: Supposons que, pour un entier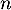 ,
, 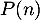 soit vraie,
c'est-à-dire
soit vraie,
c'est-à-dire 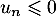 .
.
On a, au rang suivant,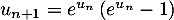 ,
,
avec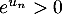 , et comme
, et comme 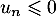 donc, en appliquant la fonction exponentielle qui est croissante,
on obtient
donc, en appliquant la fonction exponentielle qui est croissante,
on obtient 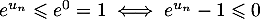 .
.
Ainsi,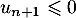 et la propriété
et la propriété 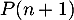 est donc aussi vraie.
est donc aussi vraie.
Conclusion: On vient donc de démontrer, d'après le principe de récurrence, que les propriétés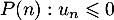 sont vraies pour tout entier
sont vraies pour tout entier 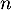 .
.
- On a donc montré que la suite
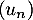 est croissante, à la question 2. b), et qu'elle est majorée par 0 à la question précédente;
on en déduit donc qu'elle est convergente vers une limite
est croissante, à la question 2. b), et qu'elle est majorée par 0 à la question précédente;
on en déduit donc qu'elle est convergente vers une limite 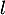 .
.
D'après le théorème du point fixe, on sait de plus que cette limite vérifie
![\[f(l)=l\iff e^{2l}-e^l=l\iff e^{2l}-e^l-l=0\iff g(l)=0\]](/Generateur-Devoirs/TS/ChapExponentielle/exSRexp_c/58.png)
On a vu que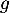 a pour minimum 0, et donc
a pour minimum 0, et donc 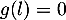 a pour unique solution
a pour unique solution 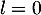 , et on en déduit donc que
, et on en déduit donc que
![\[\lim_{n\to+\infty}u_n=0\]](/Generateur-Devoirs/TS/ChapExponentielle/exSRexp_c/62.png)
- On vient de trouver à la question précédente,
que
Cacher la correction
Tags:ExponentielleSuites
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
