Bac 2012 (Centres étrangers) - Résolution d'une équation avec exponentielle
Exercice corrigé - Spécialité maths, terminale générale
(Bac S, Centres étrangers 2012, 6 points)
On considère l'équation (E) d'inconnue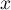 réelle :
réelle :  .
.
Partie A : Conjecture graphique
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction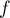 définie sur
définie sur  par
par 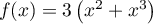 telles que les affiche une calculatrice dans un même repère orthogonal.
telles que les affiche une calculatrice dans un même repère orthogonal.
![\[
\psset{xunit=1.0cm,yunit=1.0cm,algebraic=true,dotstyle=o,dotsize=3pt 0,linewidth=0.8pt,arrowsize=3pt 2,arrowinset=0.25}
\begin{pspicture*}(-7,-6)(7,6)
\psaxes[labelFontSize=\scriptstyle,xAxis=true,yAxis=true,Dx=1,Dy=1,ticksize=-2pt 0,subticks=2]{->}(0,0)(-7,-6)(7,6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-7.0}{7.0}{EXP(x)}
\psplot[plotpoints=2000,linewidth=1.25pt]{-7.0}{7.0}{3*(x^2+x^3)}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/6.png)
À l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
Partie B : étude de la validité de la conjecture graphique
Correction
On considère l'équation (E) d'inconnue
Partie A : Conjecture graphique
Le graphique ci-dessous donne la courbe représentative de la fonction exponentielle et celle de la fonction
![\[
\psset{xunit=1.0cm,yunit=1.0cm,algebraic=true,dotstyle=o,dotsize=3pt 0,linewidth=0.8pt,arrowsize=3pt 2,arrowinset=0.25}
\begin{pspicture*}(-7,-6)(7,6)
\psaxes[labelFontSize=\scriptstyle,xAxis=true,yAxis=true,Dx=1,Dy=1,ticksize=-2pt 0,subticks=2]{->}(0,0)(-7,-6)(7,6)
\psplot[plotpoints=2000,linewidth=1.25pt,linecolor=blue]{-7.0}{7.0}{EXP(x)}
\psplot[plotpoints=2000,linewidth=1.25pt]{-7.0}{7.0}{3*(x^2+x^3)}
\end{pspicture*}
\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/6.png)
À l'aide du graphique ci-dessus, conjecturer le nombre de solutions de l'équation (E) et leur encadrement par deux entiers consécutifs.
Partie B : étude de la validité de la conjecture graphique
-
- Étudier selon les valeurs de
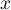 , le signe de
, le signe de  .
.
- En déduire que l'équation (E)n'a pas de solution sur l'intervalle
![$]-\infty~;~-1]$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/9.png) .
.
- Vérifier que 0 n'est pas solution de (E).
- Étudier selon les valeurs de
- On considère la fonction
 , définie pour tout nombre réel de
, définie pour tout nombre réel de ![$]-1~;~0[\cup]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/11.png) par :
par :
![\[h(x)=\ln 3+\ln\left(x^2\right)+\ln(1+x)-x.\]](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/12.png)
Montrer que, sur![$]-1~;~0[\: \cup\: ]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/13.png) , l'équation (E) équivaut à
, l'équation (E) équivaut à 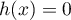 .
.
-
- Etudier les limites de
 en
en 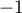 ,
, 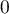 et
et 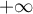 .
.
- Montrer que, pour tout réel
 appartenant à
appartenant à ![$]-1~;~0[~\cup~]0~;~+\infty[$](/Generateur-Devoirs/TS/ChapLogarithme/ex112.CE/20.png) , on a:
, on a:
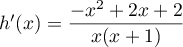
- Déterminer les variations de la fonction
 .
.
- Déterminer le nombre de solutions de l'équation
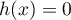 et donner une valeur arrondie au centième de chaque solution.
et donner une valeur arrondie au centième de chaque solution.
- Conclure quant à la conjecture de la partie A.
- Etudier les limites de
Correction
Tag:Exponentielle
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
