Oral de Bac - Calcul d'intégrale, linéarité
Exercice corrigé - Spécialité maths, terminale générale
On cherche à calculer l'intégrale 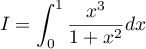 .
.
- Calculer l'intégrale
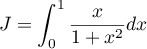 .
.
- Calculer
 .
.
- En déduire la valeur de
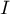 .
.
Correction
Cacher la correction
-
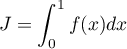 , avec
, avec 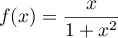 .
On reconnaît "presque" une expression de la forme
.
On reconnaît "presque" une expression de la forme 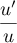 avec
avec 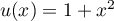 , et donc
, et donc 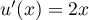 , d'où
, d'où
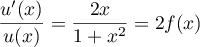 .
.
Ainsi,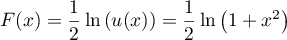 est une
primitive de
est une
primitive de 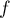 , et on a
, et on a
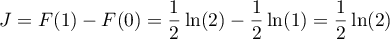
- Par linéraité de l'intégrale, on a
![\begin{array}{ll}
I+J&\dsp=\int_0^1 \dfrac{x^3}{1+x^2}dx+\int_0^1 \dfrac{x}{1+x^2}dx\\[.5cm]
&\dsp=\int_0^1 \lp\dfrac{x^3}{1+x^2}+\dfrac{x}{1+x^2}\right) dx\\[.5cm]
&\dsp=\int_0^1 \dfrac{x^3+x^2}{1+x^2}dx\\[.5cm]
&\dsp=\int_0^1 \dfrac{x\left( x^2+1\rp}{1+x^2}dx\\[.5cm]
&\dsp=\int_0^1 x\,dx
\enar](/Generateur-Devoirs/TS/ChapIntegration/exOral01_c/10.png)
or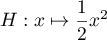 est une primitive de
est une primitive de 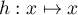 ,
et donc,
,
et donc,
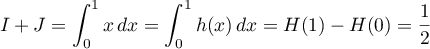
- D'après ce qui précède, on a donc,
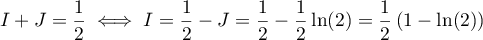 .
.
Cacher la correction
Tag:Intégrales
Voir aussi:
Quelques devoirs
intégration, Calculs d'intégrales - Suite d'intégrales (Bac S, 19 juin 2014) - Dimensionnement d'un récupérateur d'eau (Bac S - Amérique du nord, 1er juin 2016)
intégration, Calculs d'intégrales - Aire sous une courbe (Bac S - métropole, 11 septembre 2014) - Aire entre deux courbes (Bac S, juin 2008)
sur les intégrales: calcul d'intégrales, suite d'intégrales, et un calcul de volume
sur les intégrales: calcul d'intégrales, suite d'intégrales
