Calculs de dérivées
Exercice corrigé - Spécialité maths, terminale générale
Calculer la dérivée des fonctions suivantes (simplifier l'expression bien sûr, une seule fraction, expression factorisée …):
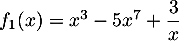 ;
;
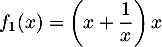 ;
;
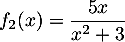 ;
;
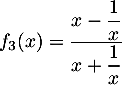
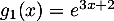 ;
;
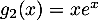 ;
;
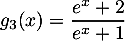 ;
;
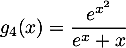
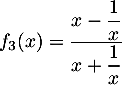
Correction
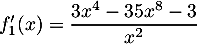 ;
;
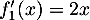 ;
;
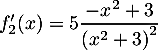 ;
;
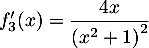
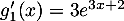 ;
;
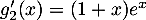 ;
;
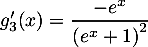 ;
;
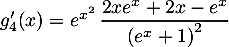
Voir aussi: calculs de dérivées, exercices corrigés et détaillés et calculs de dérivées avec exponentielles.
Cacher la correction
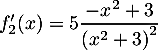 ;
;
Voir aussi: calculs de dérivées, exercices corrigés et détaillés et calculs de dérivées avec exponentielles.
Cacher la correction
Tag:Fonctions
Voir aussi:
