logarithme, asymptote oblique et position relative et calcul d'aire
Exercice corrigé - Spécialité maths, terminale générale
On considère la fonction 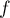 définie sur l'intervalle
définie sur l'intervalle 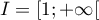 par:
par: 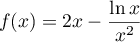 .
.
On note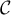 sa courbe représentative.
sa courbe représentative.
Correction
On note
- Montrer que la droite
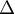 d'équation
d'équation 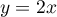 est une asymptote à
est une asymptote à 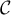 en
en 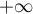 .
.
- Etudier la position relative de la courbe
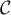 et de la
droite
et de la
droite 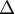 .
.
- On admet que
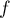 est strictement croissante sur
est strictement croissante sur 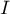 .
Tracer dans un repère l'allure de
.
Tracer dans un repère l'allure de 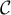 .
.
On prendra comme unités: 2cm sur l'axe des abscisses et 1cm sur l'axe des ordonnées. - Soit
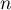 un entier naturel non nul.
un entier naturel non nul.
On considère le domaine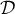 du plan compris entre la
courbe
du plan compris entre la
courbe 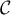 , la droite
, la droite 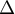 , et les
droites d'équations respectives
, et les
droites d'équations respectives 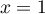 et
et 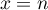 .
.
- Justifier que cette aire, exprimée en
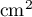 , est donnée
par:
, est donnée
par:
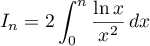 .
.
- Montrer que la fonction
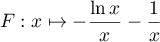 est une primitive de la fonction
est une primitive de la fonction 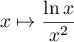 sur
sur
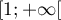 .
.
- En déduire une expression de
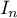 en fonction de
en fonction de 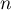 .
.
- Calculer la limite de l'aire du domaine
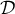 quand
quand 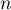 tend vers
tend vers 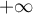 .
.
- Justifier que cette aire, exprimée en
Correction
Tags:IntégralesFonctionsPrimitive
Voir aussi:
Quelques devoirs
intégration, Calculs d'intégrales - Suite d'intégrales (Bac S, 19 juin 2014) - Dimensionnement d'un récupérateur d'eau (Bac S - Amérique du nord, 1er juin 2016)
intégration, Calculs d'intégrales - Aire sous une courbe (Bac S - métropole, 11 septembre 2014) - Aire entre deux courbes (Bac S, juin 2008)
sur les intégrales: calcul d'intégrales, suite d'intégrales, et un calcul de volume
sur les intégrales: calcul d'intégrales, suite d'intégrales
