Réglage d'une machine dans une usine

Exercice corrigé - maths en seconde générale

Énoncé

Dans une usine, une machine produit des pièces de différents diamètres.

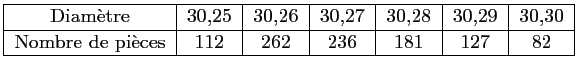
On a mesuré le diamètre, en mm, de 1000 de ces pièces. Le tableau suivant donne les résultats obtenus:

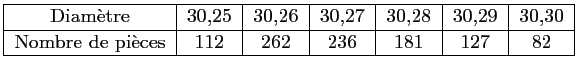
$\displaystyle \begin{tabular}{\vert c\vert*7{c\vert}}\hline Diam\\lq etre & 30,25... ... Nombre de pi\\lq eces & 112 & 262 & 236 & 181 & 127 & 82 \\ \hline \end{tabular}$

1. Déterminer le mode, la médiane et l'étendue de cette série.

2. Calculer le diamètre moyen de ces pièces.

3. On considère que la machine est déréglée si au moins 20% des pièces ont un diamètre qui s'écarte du diamètre moyen de plus de 0,02 mm.
La machine doit-elle ici être réglée ?



Correction

Correction

1. 30,26 est la valeur modale de cette série.

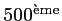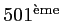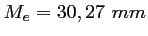L'effectif total est 1000, la médiane est donc la moyenne de la $ 500^{\mbox{\scriptsize {\\lq eme}}}$ valeur et de la $ 501^{\mbox{\scriptsize {\\lq eme}}}$ valeur. La médiane est donc la moyenne des valeurs 30,27 et 30,27, soit $ M_e=30,27\ mm$ .

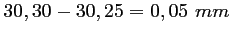L'étendue de cette série est $ 30,30 - 30,25=0,05\ mm$ .

2. Le diamètre moyen des pièces est:


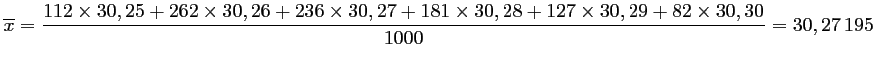
$ \displaystyle \overline{x}=\frac{112\times 30,25+262\times 30,26+236\times 30,27+181\times 30,28+127\times 30,29+82\times 30,30}{1000}=30,27\,195$


3. Les pièces considérées comme défectueuses sont celles qui ont un diamètre inférieur à

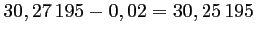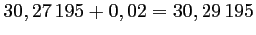$ 30,27\,195-0,02=30,25\,195$ et celles qui ont un diamètre supérieur à $ 30,27\,195+0,02=30,29\,195$ .

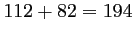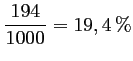Il y a ici $ 112+82=194$ telles pièces, soit un pourcentage de $ \displaystyle \frac{194}{1000}=19,4\,\%$ :

la machine n'a pas besoin d'être réglée.



Tag:Statistiques

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs