Suite récurrente et fonction logarithme
Colle de mathématiques
Sujet de colle de maths:- SuitesSuites
- RécurrenceDémonstration par récuurrence
- LimiteLimites de suites et de fonctions
Énoncé du sujet
Soit  la suite définie par son premier terme
la suite définie par son premier terme 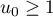 et par la relation de récurrence
et par la relation de récurrence  où
où 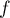 est la fonction définie par l'expression
est la fonction définie par l'expression 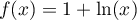 .
.
- Démontrer que la suite est bien définie et qu'elle est minorée par 1.
- Étudier le signe de
 sur
sur 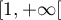 .
.
- Étudier la monotonie de
 .
.
- En déduire que
 est convergente, et donner sa limite.
est convergente, et donner sa limite.
Correction
Correction
- On démontre cette propriété par récurrence: soit pour
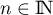 , la propriété
, la propriété 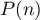 : "
: "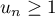 ".
Démontrer ces propriétés montrera par la même occasion que la suite
".
Démontrer ces propriétés montrera par la même occasion que la suite 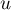 est bien définie puisque
est bien définie puisque 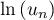 sera alors bien défini.
sera alors bien défini.
Initialisation: on sait d'après l'énoncé que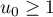 , ce qui est exactement la propriété
, ce qui est exactement la propriété  .
.
Hérédité: soit tel que
tel que 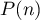 est vraie, c'est-à-dire tel que
est vraie, c'est-à-dire tel que 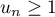 .
.
On a alors, puisque la fonction logarithme est croissante, ,
et donc
,
et donc 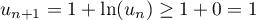 .
.
Ainsi,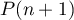 est encore vraie.
est encore vraie.
Conclusion: d'après le principe de récurrence,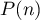 est vraie pour tout entier
est vraie pour tout entier 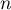 .
.
- On pose
 . Pour trouver le signe de
. Pour trouver le signe de 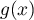 on peut penser à étudier la fonction.
on peut penser à étudier la fonction.
La fonction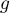 est dérivable sur
est dérivable sur 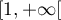 , avec
, avec 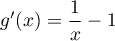 .
.
Pour , on a
, on a  et donc
et donc 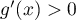 , et donc
, et donc 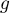 est strictement décroissante sur l'intervalle
est strictement décroissante sur l'intervalle  .
.
Puisque , on en déduit que
, on en déduit que 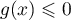 pour tout
pour tout  .
Ainsi, on a
.
Ainsi, on a 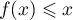 pour tout
pour tout  .
.
- Pour totu entier
 , puisque
, puisque  , on a alors que
, on a alors que 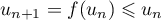 , ce qui montre que la suite
, ce qui montre que la suite 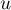 est décroissante.
est décroissante.
- La suite est décroissante et minorée par 1, et elle est donc convergente vers une limite
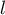 qui vérifie de plus l'équation
qui vérifie de plus l'équation
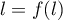 .
.
On a de plus, comme pour tout
pour tout 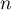 ,
, 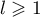 .
.
D'après la question précédent, on a vu que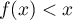 pour tout
pour tout 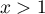 .
Donc si
.
Donc si 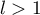 , on a
, on a  ce qui est impossible.
On doit donc nécessairement avoir
ce qui est impossible.
On doit donc nécessairement avoir 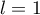
Tags:SuitesRécurrenceLimite
Autres sujets au hasard:

Voir aussi: