Divergence de la série harmonique
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
Soit la suite 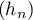 définie par
définie par
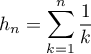 .
.
Montrer que, pour tout entier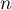 ,
, 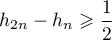 .
.
En déduire la limite de .
.
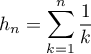 .
.
Montrer que, pour tout entier
En déduire la limite de
Correction
Calcul direct. On cherche à minorer une somme de fractions, ou encore à majorer les dénominateurs de ces fractions,
![\[h_{2n}-h_n=\dsp\sum_{k=n+1}^{2n}\dfrac1k\]](/Generateur-Devoirs/Colles/Suites/ex8_c/1.png)
Pour chaque terme de cette somme,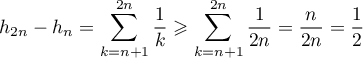 et donc
et donc
 , et ainsi, en sommant ces
, et ainsi, en sommant ces 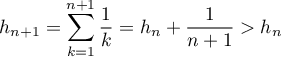 termes
termes
![\[\begin{array}{ll}h_{2n}-h_n&=\dsp\sum_{k=n+1}^{2n}\dfrac1k\\[1em]
&\geqslant\dsp\sum_{k=n+1}^{2n}\dfrac1{2n}=\dfrac{n}{2n}=\dfrac12\enar\]](/Generateur-Devoirs/Colles/Suites/ex8_c/5.png)
Par récurrence. On note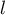 et la propriété
et la propriété 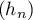 :
:  pour
pour 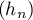
Initialisation: Pour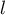 ,
, 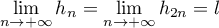 et la propriété est donc bien vraie initialement.
et la propriété est donc bien vraie initialement.
Hérédité: supposons que, pour un certain entier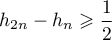 , le propriété
, le propriété
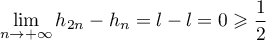 :
: 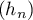 soit vraie.
soit vraie.
Alors,
![\[\begin{array}{ll}u_{n+1}&=h_{2n+1}-h_{n+1}\\[.8em]
&=\dsp\sum_{k=1}^{2(n+1)}\dfrac1k-\sum_{k=1}^{n+1}\dfrac1k\\[.7em]
&=u_n+\dfrac1{2n+2}+\dfrac1{2n+1}-\dfrac1{n+1}
\enar\]](/Generateur-Devoirs/Colles/Suites/ex8_c/15.png)
et donc, comme par hypothèse de récurrence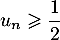 , on a
, on a
![\[u_{n+1}\geqslant\dfrac12+\dfrac1{2n+2}+\dfrac1{2n+1}-\dfrac1{n+1}\]](/Generateur-Devoirs/Colles/Suites/ex8_c/17.png)
Il reste donc à démontrer que cette dernière somme de fraction est positive:
![\[\begin{array}{ll}\dfrac1{2n+2}+\dfrac1{2n+1}-\dfrac1{n+1}
&=\dfrac{(2n+1)(n+1)+(2n+2)(n+1)-(2n+2)(2n+1)}{(2n+2)(2n+1)(n+1)}\\[.8em]
&=\dfrac{(n+1)\Bigl((2n+1)+(2n+2)-2(2n+1) \Bigr)}{(2n+2)(2n+1)(n+1)}\\[.8em]
&=\dfrac{(n+1)\Bigl( 1 \Bigr)}{(2n+2)(2n+1)(n+1)} > 0
\enar\]](/Generateur-Devoirs/Colles/Suites/ex8_c/18.png)
et on a donc bien trouvé que
![\[u_{n+1}\geqslant\dfrac12+0\]](/Generateur-Devoirs/Colles/Suites/ex8_c/19.png)
c'est-à-dire que la propriété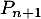 est aussi vraie.
est aussi vraie.
Conclusion: on vient donc de démontrer, d'après le principe de récurrence que, pour tout entier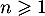 , on a
, on a
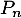 :
: 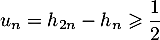
La suite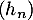 est clairement strictement croissante
car
est clairement strictement croissante
car
![\[h_{n+1}-h_n=\dfrac1{n+1}>0\]](/Generateur-Devoirs/Colles/Suites/ex8_c/25.png)
et donc d'après le théorème de limite monotone, soit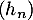 est majorée et convergente vers un réel
est majorée et convergente vers un réel 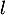 ,
soit
,
soit 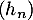 diverge vers
diverge vers 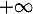 .
.
Supposons que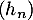 converge vers
converge vers 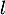 ,
alors
,
alors 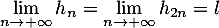 ,
et alors, comme
,
et alors, comme 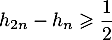 ,
on devrait avoir par passage à la limite,
,
on devrait avoir par passage à la limite,
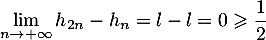 ,
ce qui est absurde.
,
ce qui est absurde.
On en déduit finalement que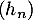 diverge nécessairement vers
diverge nécessairement vers 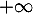 .
.
Correction
On peut démontrer cette minoration de deux façons (au moins): par un calcul direct ou par récurrence.Calcul direct. On cherche à minorer une somme de fractions, ou encore à majorer les dénominateurs de ces fractions,
![\[h_{2n}-h_n=\dsp\sum_{k=n+1}^{2n}\dfrac1k\]](/Generateur-Devoirs/Colles/Suites/ex8_c/1.png)
Pour chaque terme de cette somme,
![\[\begin{array}{ll}h_{2n}-h_n&=\dsp\sum_{k=n+1}^{2n}\dfrac1k\\[1em]
&\geqslant\dsp\sum_{k=n+1}^{2n}\dfrac1{2n}=\dfrac{n}{2n}=\dfrac12\enar\]](/Generateur-Devoirs/Colles/Suites/ex8_c/5.png)
Par récurrence. On note
Initialisation: Pour
Hérédité: supposons que, pour un certain entier
Alors,
![\[\begin{array}{ll}u_{n+1}&=h_{2n+1}-h_{n+1}\\[.8em]
&=\dsp\sum_{k=1}^{2(n+1)}\dfrac1k-\sum_{k=1}^{n+1}\dfrac1k\\[.7em]
&=u_n+\dfrac1{2n+2}+\dfrac1{2n+1}-\dfrac1{n+1}
\enar\]](/Generateur-Devoirs/Colles/Suites/ex8_c/15.png)
et donc, comme par hypothèse de récurrence
Il reste donc à démontrer que cette dernière somme de fraction est positive:
![\[\begin{array}{ll}\dfrac1{2n+2}+\dfrac1{2n+1}-\dfrac1{n+1}
&=\dfrac{(2n+1)(n+1)+(2n+2)(n+1)-(2n+2)(2n+1)}{(2n+2)(2n+1)(n+1)}\\[.8em]
&=\dfrac{(n+1)\Bigl((2n+1)+(2n+2)-2(2n+1) \Bigr)}{(2n+2)(2n+1)(n+1)}\\[.8em]
&=\dfrac{(n+1)\Bigl( 1 \Bigr)}{(2n+2)(2n+1)(n+1)} > 0
\enar\]](/Generateur-Devoirs/Colles/Suites/ex8_c/18.png)
et on a donc bien trouvé que
c'est-à-dire que la propriété
Conclusion: on vient donc de démontrer, d'après le principe de récurrence que, pour tout entier
La suite
et donc d'après le théorème de limite monotone, soit
Supposons que
On en déduit finalement que
Tags:SuitesSommesLimite
Autres sujets au hasard:

Voir aussi: