Convergence de sommes de type Riemann
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
- Soit
![$f:[0;1]\to\R$](/Generateur-Devoirs/Colles/Suites/ex19/1.png) telle
que
telle
que  .
.
Montrer que
![\[\forall\epsilon>0,\exists N\n\N,\forall n\geqslant N,
\left|\sum_{k=0}^n\dfrac{k}{n^2}f\lp\dfrac{k}{n^2}\rp\right|\leqslant\epsilon\]](/Generateur-Devoirs/Colles/Suites/ex19/3.png)
- Soit
![$g:[0;1]\to\R$](/Generateur-Devoirs/Colles/Suites/ex19/4.png) dérivable en 0.
Étudier la suite
dérivable en 0.
Étudier la suite 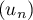 définie par
définie par
![\[u_n=\sum_{k=0}^n g\kp\dfrac{k}{n^2}\rp\]](/Generateur-Devoirs/Colles/Suites/ex19/6.png)
Correction
Correction
- Si on arrive à majorer "convenablement"
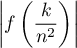 par
par  ,
on aura alors par l'inégalité triangulaire
,
on aura alors par l'inégalité triangulaire
![\[\begin{array}{ll}\left|\dsp\sum_{k=0}^n\dfrac{k}{n^2}f\lp\dfrac{k}{n^2}\rp\right|
&\leqslant\dsp\sum_{k=0}^n\dfrac{k}{n^2}f\left|\lp\dfrac{k}{n^2}\rp\right|\\[.7em]
&\leqslant\displaystyle M\sum_{k=0}^n\dfrac{k}{n^2}\\[.7em]
&\leqslant\displaystyle M\sum_{k=0}^n\dfrac{n}{n^2}
=M\dfrac1n\sum_{k=0}^n1=M
\enar\]](/Generateur-Devoirs/Colles/Suites/ex19_c/3.png)
D'après ce calcul, il suffit donc d'arriver à majorer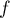 par
par  , ce qui est possible d'après l'hypothèse sur la limite de
, ce qui est possible d'après l'hypothèse sur la limite de 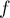 en 0.
en 0.
Plus précisément, soit , alors il existe
, alors il existe 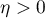 tel que, pour tout
tel que, pour tout  ,
,  .
.
Pour tout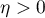 , soit donc
, soit donc  tel que
tel que 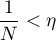 , alors,
pour tout
, alors,
pour tout 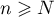 et tout
et tout 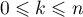 , on a
, on a
![\[\dfrac{k}{n^2}\leqslant\dfrac{n}{n^2}=\dfrac1n\leqslant\dfrac1N\leqslant\eta
\Longrightarrow \left|f\lp\dfrac{k}{n^2}\rp\right|\leqslant\epsilon\]](/Generateur-Devoirs/Colles/Suites/ex19_c/16.png)
Le premier calcul ci-dessus permet alors de conclure que,
![\[\begin{array}{ll}\left|\dsp\sum_{k=0}^n\dfrac{k}{n^2}f\lp\dfrac{k}{n^2}\rp\right|\leqslant\epsilon\]](/Generateur-Devoirs/Colles/Suites/ex19_c/17.png)
On déduit de ce résultat que
![\[\lim_{n\to+\infty}\sum_{k=0}^n\dfrac{k}{n^2}f\lp\dfrac{k}{n^2}\rp=0\]](/Generateur-Devoirs/Colles/Suites/ex19_c/18.png)
- Comme la fonction
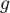 est dérivable en 0,
on a l'approximation affine (ou DL d'ordre 1),
est dérivable en 0,
on a l'approximation affine (ou DL d'ordre 1),
![\[g(x)=g(0)+xg'(0)+x\phi(x)\ ,\text{ o\`u } \lim_{x\to0}\phi(x)=0\]](/Generateur-Devoirs/Colles/Suites/ex19_c/20.png)
On a alors en utilisant ce développement,
![\[\begin{array}{ll}u_n&=\dsp\sum_{k=0}^n \Bigl( g(0)+\dfrac{k}{n^2}g'(0)+\dfrac{k}{n^2}\phi\lp\dfrac{k}{n^2}\rp\Bigr) \\[.8em]
&=(n+1)g(0)+\dfrac{n(n+1)}{2n^2}g'(0)+\dsp\sum_{k=0}^n\dfrac{k}{n^2}\phi\lp\dfrac{k}{n^2}\right)
\enar\]](/Generateur-Devoirs/Colles/Suites/ex19_c/21.png)
D'après la question précédente, la dernière somme tend vers 0, et on a donc,- si
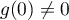 ,
, 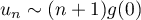 et
et 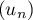 diverge vers
diverge vers 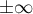 selon le signe de
selon le signe de  ;
;
- si
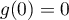 , alors
, alors  et donc
et donc
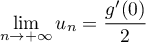
- si
Tags:SuitesSommesLimite
Autres sujets au hasard:

Voir aussi: