Somme matrice plus nilpotente
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
Énoncé du sujet
Soit une matrice 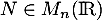 pour laquelle il existe
pour laquelle il existe 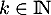 tel que
tel que 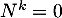 .
.
- Donner un exemple d'une telle matrice.
- Trouver les valeurs propres de
 .
.
- La matrice
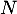 est-elle diagonalisable ?
est-elle diagonalisable ?
- Soit
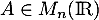 une autre matrice.
une autre matrice.
- On suppose que
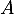 commute avec
commute avec 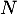 .
Montrer que
.
Montrer que 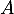 est inversible si et seulement si
est inversible si et seulement si 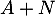 est inversible.
est inversible.
- Montrer que ce n'est plus vrai si
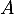 et
et 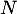 ne commutent pas.
(on pourra chercher un contre-exemple avec
ne commutent pas.
(on pourra chercher un contre-exemple avec  ).
).
- On suppose que
- On suppose ici que
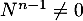 et
et 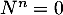 .
On prend
.
On prend 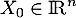 tel que
tel que 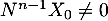 .
Montrer que
.
Montrer que
 forme une base de
forme une base de 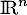 .
Écrire
.
Écrire 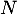 dans cette base.
dans cette base.
Correction
Correction
Oral ENS ULM - 2021- La matrice nulle convient.
On peut aussi prendre par exemple la matrice
![\[N=\lp\begin{array}{cccc}
0&0&\dots&1\\
0&0&\dots&0\\
\vdots&\vdots&\ddots&\vdots\\
0&0&\dots&0
\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/1.png)
pour laquelle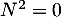 .
.
- Soit
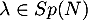 , alors il existe
, alors il existe 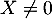 tel que
tel que 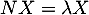 ,
et donc, en multipliant plusieurs fois par
,
et donc, en multipliant plusieurs fois par 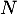 , on doit avoir
, on doit avoir
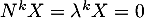 .
.
Ainsi, comme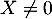 , il vient
, il vient 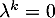 donc
donc 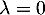 .
.
En d'autres termes, on vient de trouver que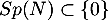 .
.
Réciproquement, 0 est une valeur propre de , car
, car 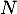 n'est pas inversible
(sinon
n'est pas inversible
(sinon 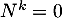 le serait aussi, ce qui n'est pas le cas),
et donc
le serait aussi, ce qui n'est pas le cas),
et donc 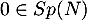 .
.
On a donc trouvé que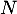 a une unique valeur propre
a une unique valeur propre 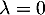 ,
ou encore que
,
ou encore que 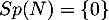 .
.
- Si
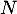 était diagonalisable, elle serait semblable à
était diagonalisable, elle serait semblable à 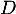 diagonale avec uniquement
diagonale avec uniquement 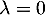 sur la diagonale donc
sur la diagonale donc 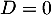 , et alors
, et alors
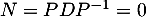 .
La seule matrice nilpotente et diagonalisable est la matrice nulle.
.
La seule matrice nilpotente et diagonalisable est la matrice nulle.
-
-
- Supposons
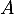 inversible.
inversible.
Soit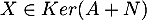 . On a alors
. On a alors 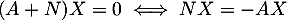 ,
et donc, en appliquant
,
et donc, en appliquant 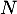 et en commutant:
et en commutant:
![\[N^2X=-NAX=-ANX=-A(-AX)=A^2X\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/28.png)
Ensuite, en itérant, il vient
![\[N^kX=(-1)^kA^kX=0\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/29.png)
Or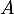 est inversible donc
est inversible donc 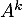 aussi donc
aussi donc 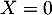 .
.
On a ainsi montré que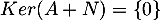 , ou encore,
en d'autres termes, que
, ou encore,
en d'autres termes, que 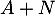 est injective, donc bijective ou encore inversible.
est injective, donc bijective ou encore inversible.
- Réciproquement, supposons que
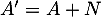 inversible.
inversible.
On a alors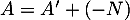 et, comme
et, comme 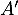 commute avec
commute avec 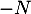 et que
et que 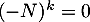 ,
on applique l'implication précédente à
,
on applique l'implication précédente à 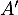 et
et 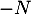 et on obtient que
et on obtient que 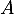 inversible.
inversible.
- Supposons
- Pour matrice nilpotente, comme proposé à la première question, on peut choisir
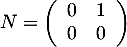 .
.
On prend ensuite prendre par exemple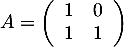 .
.
-
- On peut commencer par montrer que cette famille est libre:
soit
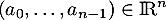 tel que
tel que
![\[\sum_{i=0}^{n-1} a_iN^iX_0=0\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/46.png)
En appliquant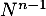 , tous les termes de la somme s'annulent sauf le premier,
à savoir
, tous les termes de la somme s'annulent sauf le premier,
à savoir
![\[a_0N^{n-1}X_0=0\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/48.png)
et, comme , on obtient donc
, on obtient donc 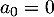 , et la somme se réécrit
, et la somme se réécrit
![\[\sum_{i=1}^{n-1} a_iN^iX_0=0\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/51.png)
On applique maintenant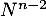 , et il reste cette fois
, et il reste cette fois
![\[a_1N^{n-1}X_0=0\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/53.png)
d'où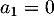 .
.
En répétant ce raisonnement, on trouve ainsi, successivement, .
En d'autres termes, la famille
.
En d'autres termes, la famille
 est libre.
est libre.
Comme de plus elle est composée de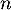 vecteurs dans un espace de dimension
vecteurs dans un espace de dimension
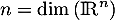 , on en déduit qu'elle est une base.
, on en déduit qu'elle est une base.
Enfin, dans cette base,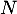 envoie chaque vecteur sur le suivant sauf le dernier dont l'image est nulle. La matrice de
envoie chaque vecteur sur le suivant sauf le dernier dont l'image est nulle. La matrice de 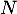 est donc
est donc
![\[\lp\begin{array}{ccccc}
0&0& \dots &0&0\\
1&0& \dots &0&0\\
0&1&\dots &0&0\\
\vdots&\vdots&\ddots&\vdots&\vdots\\
0&0&\dots&1&0\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/addMN_c/61.png)
Tag:Diagonalisation
Autres sujets au hasard:
