Vrai ou Faux
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
- MatricesMatrices
Énoncé du sujet
Vrai ou faux ?
- En dimension finie, un endomorphisme admet un nombre fini de vecteurs propres.
- Si
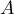 est diagonalisable, alors
est diagonalisable, alors 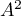 est diagonalisable.
est diagonalisable.
- Si
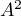 est diagonalisable, alors
est diagonalisable, alors 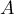 est diagonalisable.
est diagonalisable.
- La somme de deux matrices diagonalisables est diagonalisable.
Correction
Correction
- Faux. Un endomorphisme peut n'admettre aucun vecteur propre, mais s'il en admet, il y en a une infinité: si
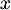 est vecteur propre, alors
est vecteur propre, alors 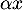 est aussi un vecteur propre pour tout
est aussi un vecteur propre pour tout 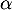 .
.
- Vrai. Si
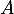 est diagonalisable, il existe
est diagonalisable, il existe 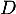 diagonale telle que
diagonale telle que 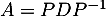 avec
avec 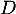 , et on a alors
, et on a alors 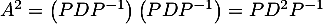 et, comme
et, comme 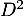 est aussi diagonale,
est aussi diagonale, 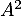 est donc diagonalisable (qui plus est dans la même base que
est donc diagonalisable (qui plus est dans la même base que 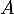 ).
).
- Non, la réciproque précédente est fausse. Il suffit par exemple de considérer une matrice nilpotente, c'est-à-dire telle que
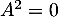 , par exemple
, par exemple 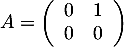 qui n'est pas diagonalisable alors que
qui n'est pas diagonalisable alors que 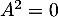 et la matrice nulle est diagonale.
et la matrice nulle est diagonale.
On peut aussi considérer la matrice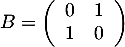 qui est telle que
qui est telle que 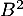 est l'identité qui est aussi diagonale.
est l'identité qui est aussi diagonale.
- Faux. Il suffit de considérer deux matrices diagonalisables (triangulaire, avec des valeurs diagonales, et donc valeurs propres, distinctes par exemple), et dont la somme est nilpotente, par exemple:
![\[A=\lp\begin{array}{cc}1&1\\0&2\enar\right) \text{ et }
B=\lp\begin{array}{cc}-1&0\\0&-2\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/Vrai-faux_c/17.png)
Tags:DiagonalisationMatrices
Autres sujets au hasard:

Voir aussi: