Somme directe des noyau et image d'endomorphismes définis par compositions circulaires
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Soit 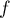 ,
, 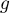 et
et 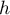 trois endomorphismes d'un même espace vectoriel
trois endomorphismes d'un même espace vectoriel 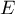 tels que
tels que
 ,
,  et
et 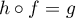 .
On note
.
On note  .
.
Montrer que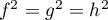 puis que
puis que 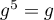 .
.
Prouvez alors que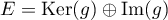 .
.
Montrer que
Prouvez alors que
Correction
![\[\begin{array}{ll}
f^2&=f\circ f\\
&=\left( g\circ h\rp\circ f\\
&=g\circ\left( h\circ f\rp\\
&=g\circ g=g^2
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL9_c/1.png)
En permuttant circulairement, on a de même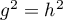 et donc
et donc
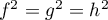 .
.
On a alors
![\[\begin{array}{ll}
g^5&=g^3\circ g^2\\
&=g^3\circ h^2\\
&=g^2\circ\left( g\circ h\rp\circ h\\
&=g^2\circ f\circ h\\
&=h^2\circ f\circ h\\
&=h\circ\left( h\circ f\rp\circ h\\
&=h\circ g\circ h\\
&=h\circ f\\
&=g
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL9_c/4.png)
D'après la relation précédente, on a pour tout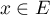 ,
,
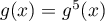 soit
soit 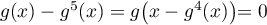 ,
c'est-à-dire que
pour tout
,
c'est-à-dire que
pour tout  ,
, 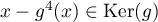 .
.
Ceci nous incite à regarder la décomposition de tout vecteur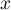 selon
selon
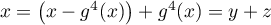 , où
comme on l'a vu (et fait exprès)
, où
comme on l'a vu (et fait exprès) 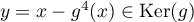 et
et 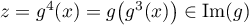 .
.
Cette décomposition montre donc que .
.
De plus, soit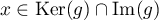 ,
alors d'une part
,
alors d'une part 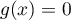 ,
et d'autre part, il existe
,
et d'autre part, il existe 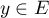 tel que
tel que
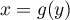 ,
donc aussi
,
donc aussi 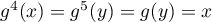 or
or 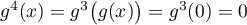 et donc
et donc  d'où
d'où
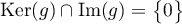 et donc la somme est directe:
et donc la somme est directe:
![\[E=\text{Ker}(g)\oplus\text{Im}(g)\]](/Generateur-Devoirs/Colles/Applin/exAL9_c/23.png)
Correction
On a![\[\begin{array}{ll}
f^2&=f\circ f\\
&=\left( g\circ h\rp\circ f\\
&=g\circ\left( h\circ f\rp\\
&=g\circ g=g^2
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL9_c/1.png)
En permuttant circulairement, on a de même
On a alors
![\[\begin{array}{ll}
g^5&=g^3\circ g^2\\
&=g^3\circ h^2\\
&=g^2\circ\left( g\circ h\rp\circ h\\
&=g^2\circ f\circ h\\
&=h^2\circ f\circ h\\
&=h\circ\left( h\circ f\rp\circ h\\
&=h\circ g\circ h\\
&=h\circ f\\
&=g
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL9_c/4.png)
D'après la relation précédente, on a pour tout
Ceci nous incite à regarder la décomposition de tout vecteur
Cette décomposition montre donc que
De plus, soit
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: