Endomorphisme défini par l'image de la base canonique
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Soit 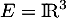 . On note
. On note 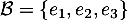 la base canonique de
la base canonique de 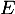 et
et 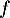 l'endomorphisme de
l'endomorphisme de 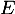 défini par la donnée des images des vecteurs de la base :
défini par la donnée des images des vecteurs de la base :
![\[\begin{array}{lcl}f(e_1) &=& -2e_1 +2e_3 \\ f(e_2)&=&3e_2 \\ f(e_3)&=&-4e_1 + 4e_3\enar\]](/Generateur-Devoirs/Colles/Applin/exALImBC/6.png)
![\[\begin{array}{lcl}f(e_1) &=& -2e_1 +2e_3 \\ f(e_2)&=&3e_2 \\ f(e_3)&=&-4e_1 + 4e_3\enar\]](/Generateur-Devoirs/Colles/Applin/exALImBC/6.png)
- Déterminer une base de
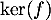 .
.
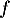 est-il injectif? peut-il être surjectif? Pourquoi?
est-il injectif? peut-il être surjectif? Pourquoi?
- Déterminer une base de
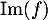 . Quel est le rang de
. Quel est le rang de  ?
?
- Montrer que
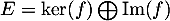 .
.
Correction
Correction
- On commence par chercher l'expression de
 .
.
On décompose les vecteurs de sur la base canonique:
sur la base canonique:
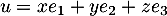 et alors, par linéarité de
et alors, par linéarité de 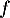
![\[\begin{array}{ll}f(x,y,z)&=f(xe_1+ye_2+ze_3)\\[.4em]&=xf(e_1)+yf(e_2)+zf(e_3)\\[.4em]
&=x\lp-2e_1+2e_3\rp+y\lp3e_2\rp+z\lp-4e_1+4e_3\rp\\[.4em]
&=(-2x-4y)e_1+3ye_2+(2x+4z)e_3\enar\]](/Generateur-Devoirs/Colles/Applin/exALImBC_c/5.png)
soit donc
![\[f(x,y,z)=(-2x-4z,3y,2x+4z)\]](/Generateur-Devoirs/Colles/Applin/exALImBC_c/6.png)
On a donc
![\[\begin{array}{ll}&(x,y,z)\in\ker(f)\\[.4em]\iff&\left\{
\begin{array}{rcl}
-2x-4z&=&0\\
3y&=&0\\
2x+4z&=&0\\
\end{array}
\right.\\[1.8em]
\iff&
\left\{
\begin{array}{rcl}
x&=&-2z\\
y&=&0\\
z&=&z
\end{array}\right.\enar\]](/Generateur-Devoirs/Colles/Applin/exALImBC_c/7.png)
Soit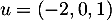 , alors on a ainsi trouvé que
, alors on a ainsi trouvé que 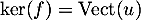 et que le vecteur
et que le vecteur  est une base de
est une base de  .
.
De plus, comme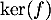 n'est pas réduit au vecteur nul, l'endomorphisme
n'est pas réduit au vecteur nul, l'endomorphisme 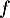 n'est pas injectif.
Enfin, comme
n'est pas injectif.
Enfin, comme 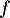 est un endomorphisme d'un espace vectoriel de dimension finie,
il n'est pas non plus surjectif, car on a alors l'équivalence
est un endomorphisme d'un espace vectoriel de dimension finie,
il n'est pas non plus surjectif, car on a alors l'équivalence
![\[f\text{ injectif}\iff f\text{ surjectif}\iff f\text{ bijectif}\]](/Generateur-Devoirs/Colles/Applin/exALImBC_c/15.png)
- D'après le théorème du rang,
![\[\text{rg}(f)+\text{dim(Ker}(f))=\text{dim}(E)=3\]](/Generateur-Devoirs/Colles/Applin/exALImBC_c/16.png)
et donc, comme on a vu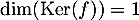 ,
on en déduit donc que
,
on en déduit donc que 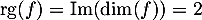 c'est-à-dire que
c'est-à-dire que 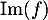 est de dimension 2.
est de dimension 2.
On sait aussi que est une famille
génératrice de
est une famille
génératrice de  . Il suffit donc d'en extraire une famille libre à deux éléments.
. Il suffit donc d'en extraire une famille libre à deux éléments.
Par exemple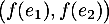 est une telle famille, libre car ces deux becteurs ne sont pas colinéaires.
C'est donc une base de
est une telle famille, libre car ces deux becteurs ne sont pas colinéaires.
C'est donc une base de 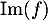 qui est de rang 2.
qui est de rang 2.
- Il suffit par exemple de montrer que la réunion d'une base de
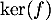 et d'une base de
et d'une base de 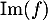 est une base de
est une base de 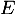 .
Autrement dit, avec les résultats précédents, il suffit de montrer que la famille
.
Autrement dit, avec les résultats précédents, il suffit de montrer que la famille
![\[\big(u,f(e_1),f(e_2)\bigl)=\big(-2,0,1),(-2,0,2),(0,3,0)\big)\]](/Generateur-Devoirs/Colles/Applin/exALImBC_c/27.png)
est une famille libre.
Soit donc trois réels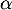 ,
, 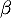 et
et 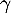 tel que
tel que
![\[\begin{array}{ll}&\alpha u+\beta f(e_1)+\gamma f(e_2)=0\\[.4em]
\iff&\la\begin{array}{rcrcrlcl}
-2\alpha&-&2\beta&&&=&0\\
&&&&3\gamma&=&0\\
\alpha&+&2\beta&&&=&0
\enar\right.\\
\iff& \alpha=\beta=\gamma=0
\enar\]](/Generateur-Devoirs/Colles/Applin/exALImBC_c/31.png)
ce qui montre que cette famille est donc bien libre et donc une base de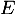 , et donc finalement que
, et donc finalement que 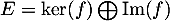 .
.
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: