Application linéaire ? Noyau et image ?
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
L'application
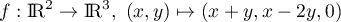 est-elle linéaire ?
est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Correction
 et
et 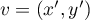 dans
dans  ,
et
,
et 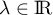 .
Alors :
.
Alors :
![\[\begin{array}{lcl}
f(u+v)&=&\big( (x+x')+(y+y'),(x+x')-2(y+y'),0)\\[.4em]
&=&\big(x+y,x-2y,0)+(x'+y',x'-2y',0)\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/5.png)
De même,
![\[\begin{array}{lcl}
f(\lambda u)&=&(\lambda x+\lambda y,\lambda x+2\lambda y,0)\\[.4em]
&=&\lambda(x+y,x+2y,0)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/6.png)
 est donc une application linéaire.
est donc une application linéaire.
De plus, soit
![\[\begin{array}{ll}
u(x,y)\in\text{Ker}(u)
&\iff f(u)=0\\[.4em]
&\iff\la\begin{array}{lcl} x+y &=& 0\\ x-2y&=&0 \\0=0 \enar\right. \\
&\iff x=y=0
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/8.png)
Ainsi, : le noyau de
: le noyau de 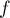 est réduit au vecteur nul et
est réduit au vecteur nul et  est injective.
est injective.
Le théorème du rang nous fournit que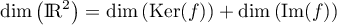 et
donc que
et
donc que  .
.
Plus précisément, Soit ,
alors il existe
,
alors il existe  tel que
tel que  ,
,
![\[\la\begin{array}{ll}
\alpha=x+y\\
\beta=x-2y\\
\gamma=0\enar\right.
\iff
\la\begin{array}{ll}
x=\dfrac{\alpha+\beta}{2}\\
y=\dfrac{\alpha-\beta}{3}\\
\gamma=0\enar\right.
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/17.png)
Ainsi, tout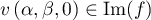 et donc
et donc
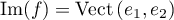 où
où
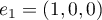 et
et 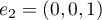 sont les deux premiers vecteurs de la base canonique de
sont les deux premiers vecteurs de la base canonique de 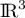 .
.
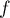 n'est donc pas surjective, donc pas non plus bijective (ce qui était clair dès le début car
n'est donc pas surjective, donc pas non plus bijective (ce qui était clair dès le début car
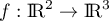 et
et 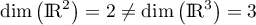 ou avec le théorème du rang).
ou avec le théorème du rang).
Correction
Soit![\[\begin{array}{lcl}
f(u+v)&=&\big( (x+x')+(y+y'),(x+x')-2(y+y'),0)\\[.4em]
&=&\big(x+y,x-2y,0)+(x'+y',x'-2y',0)\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/5.png)
De même,
![\[\begin{array}{lcl}
f(\lambda u)&=&(\lambda x+\lambda y,\lambda x+2\lambda y,0)\\[.4em]
&=&\lambda(x+y,x+2y,0)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/6.png)
De plus, soit
![\[\begin{array}{ll}
u(x,y)\in\text{Ker}(u)
&\iff f(u)=0\\[.4em]
&\iff\la\begin{array}{lcl} x+y &=& 0\\ x-2y&=&0 \\0=0 \enar\right. \\
&\iff x=y=0
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/8.png)
Ainsi,
Le théorème du rang nous fournit que
Plus précisément, Soit
![\[\la\begin{array}{ll}
\alpha=x+y\\
\beta=x-2y\\
\gamma=0\enar\right.
\iff
\la\begin{array}{ll}
x=\dfrac{\alpha+\beta}{2}\\
y=\dfrac{\alpha-\beta}{3}\\
\gamma=0\enar\right.
\enar\]](/Generateur-Devoirs/Colles/Applin/exAL1_c/17.png)
Ainsi, tout
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: