Possibilité d'un noyau ?
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Soit 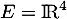 et
et 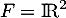 .
On considère
.
On considère  .
.
- Montrer que
 est un sous-espace vectoriel et en donner la dimension.
est un sous-espace vectoriel et en donner la dimension.
- Existe-t-il des applications linéaires de
 dans
dans  dont le noyau est
dont le noyau est  ?
?
Correction
Correction
- On a
 et donc
et donc  est bien un espace vectoriel. Il est de plus de dimension 1.
est bien un espace vectoriel. Il est de plus de dimension 1.
- Si
 était le noyau d'une application linéaire
était le noyau d'une application linéaire  de
de  dans
dans  , alors par le théorème du rang on aurait
, alors par le théorème du rang on aurait
![\[4=\dim(E)=\dim(H)+\dim(\textrm{Im}(f))=1+\dim(\textrm{Im}(f))\]](/Generateur-Devoirs/Colles/Applin/exKer_c/7.png)
Ainsi, on aurait .
.
Mais :
:  est un sous-espace vectoriel de
est un sous-espace vectoriel de
 , et donc
, et donc
![\[\text{Im}(f)\leqslant\text{dim}(\R^2)=2\]](/Generateur-Devoirs/Colles/Applin/exKer_c/12.png)
qui aboutit donc à une contradiction.
Ainsi, ne peut pas être le noyau d'un élément de
ne peut pas être le noyau d'un élément de  .
.
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: