Somme des entiers
Colle de mathématiques
Sujet de colle de maths:- SommesSommes des termes d'une suite
- RécurrenceDémonstration par récuurrence
Énoncé du sujet
Montrer par récurrence que
 .
.
En calculant la différence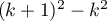 ,
trouver une démonstration directe de ce résultat.
,
trouver une démonstration directe de ce résultat.
 .
.
En calculant la différence
Correction
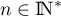 :
:
Pour ,
,
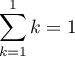 et
et 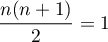 , ce qui montre que la formule est vraie initialement au rang
, ce qui montre que la formule est vraie initialement au rang  .
.
Supposons maintenant que la formule est vraie à un rang quelconque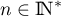 ,
c'est-à-dire
que
,
c'est-à-dire
que 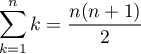 .
.
On a alors, au rang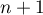 suivant:
suivant:
![\[\begin{array}{ll}\dsp\sum_{k=1}^{n+1} k
&=\dsp\sum_{k=1}^n k+(n+1)\\[.6em]
&=\dfrac{n(n+1)}{2}+(n+1) \\[.6em]
&=\dfrac{(n+1)}{2}\left( n+2\right)
\enar\]](/Generateur-Devoirs/Colles/Suites/exSommeEntiers_c/9.png)
et la formule est donc encore vraie.
On a donc montré, grâce au principe de récurrence, que pour tout entier non nul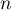 ,
,
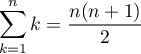 .
.
Autre démonstration: on remarque que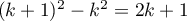 ,
et donc,
,
et donc, 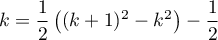 , d'où
, d'où
![\[\begin{array}{ll}
\dsp\sum_{k=1}^nk
&=\dfrac12\lp\sum_{k=1}^n(k+1)^2-\sum_{k=1}^nk^2\rp-\dfrac12\sum_{k=1}^n1 \\[1.2em]
&=\dfrac12\lp\sum_{k=2}^{n+1}k^2-\sum_{k=1}^nk^2\rp-\dfrac{n}{2} \\[1.2em]
&=\dfrac12\lp(n+1)^2-1^2\rp-\dfrac{n}{2}\\[1.2em]
&=\dfrac12\left( n^2+n \rp\\[1em]
&=\dfrac{n(n+1)}{2}
\enar\]](/Generateur-Devoirs/Colles/Suites/exSommeEntiers_c/14.png)
ce qui montre directement la formule pour tout entier non nul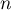 .
.
Correction
Par récurrence surPour
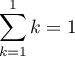 et
et Supposons maintenant que la formule est vraie à un rang quelconque
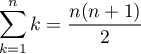 .
.
On a alors, au rang
![\[\begin{array}{ll}\dsp\sum_{k=1}^{n+1} k
&=\dsp\sum_{k=1}^n k+(n+1)\\[.6em]
&=\dfrac{n(n+1)}{2}+(n+1) \\[.6em]
&=\dfrac{(n+1)}{2}\left( n+2\right)
\enar\]](/Generateur-Devoirs/Colles/Suites/exSommeEntiers_c/9.png)
et la formule est donc encore vraie.
On a donc montré, grâce au principe de récurrence, que pour tout entier non nul
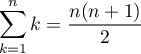 .
.
Autre démonstration: on remarque que
![\[\begin{array}{ll}
\dsp\sum_{k=1}^nk
&=\dfrac12\lp\sum_{k=1}^n(k+1)^2-\sum_{k=1}^nk^2\rp-\dfrac12\sum_{k=1}^n1 \\[1.2em]
&=\dfrac12\lp\sum_{k=2}^{n+1}k^2-\sum_{k=1}^nk^2\rp-\dfrac{n}{2} \\[1.2em]
&=\dfrac12\lp(n+1)^2-1^2\rp-\dfrac{n}{2}\\[1.2em]
&=\dfrac12\left( n^2+n \rp\\[1em]
&=\dfrac{n(n+1)}{2}
\enar\]](/Generateur-Devoirs/Colles/Suites/exSommeEntiers_c/14.png)
ce qui montre directement la formule pour tout entier non nul
Tags:SommesRécurrence
Autres sujets au hasard:

Voir aussi: