Série géométrique dérivée, loi du 1er succès et loi du nombre de succès avec une pièce

Colle de mathématiques

Sujet de colle de maths:

On possède une pièce de monnaie truquée de telle sorte que la probabilité d'obtenir pile soit 0,3.

On lance 10 fois la pièce. Quelle est la probabilité d'obtenir 3 fois pile?
On lance la pièce jusqu'à ce que l'on obtienne pile pour la première fois. Donner la probabilité de lancer 5 fois la pièce. Combien effectuera-t-on en moyenne de lancers?

Correction

Soit 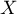la variable aléatoire égale au nombre de piles obtenus au cours des 10 lancers. 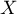est le nombre de réalisations de l'événement "le lancer donne pile" de probabilité constante 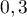au cours de 10 lancers indépendants.
suit donc la loi binomiale de paramètres et 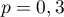, et on a donc

$P(X=3)=\binom{10}3 (0,3)^3(1-0,3)^{10-3}\simeq 0,27.$
Soit 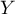le nombre de lancers effectués jusqu'à l'obtention de pile pour la première fois.
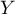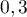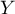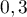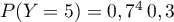est le temps d'attente de la première réalisation de l'événement "obtenir pile" de probabilité constante lors d'une suite de lancers indépendants. suit donc la loi géométrique de paramètre . On a alors $P(Y=5)=0,7^4\,0,3$ Le nombre moyen de lancers est donné par l'espérance, soit, pour la loi géométrique

$E(Y)=\dfrac1{0,3}=\frac{10}3$

soit, en moyenne, un peu plus de 3 lancers.

Autres sujets au hasard:

Voir aussi: