Espérance de l'inverse d'une loi de Poisson

Colle de mathématiques

Sujet de colle de maths:

Variables aléatoires discrètesVariables aléatoires discrètes

Énoncé du sujet

Soit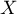

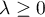une variable aléatoire suivant une loi de Poisson de paramètre $\lambda\geq0$ .
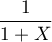Calculer l'espérance de la variable aléatoire $\dfrac1{1+X}$ .

Correction

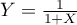Soit la variable aléatoire $Y=\frac 1{1+X}$ . Comme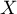

prend ses valeurs dans $\N$ ,

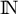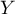prend ses valeurs dans 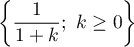$\left\{\dfrac{1}{1+k};\ k\geq 0\right\}$ avec les probabilités

$P\left(Y=\frac 1{1+k}\right)=\frac{\lambda^k}{k!}e^{-\lambda}.$

On calcule alors

$\begin{array}{lcl} E(Y)&=&\dsp\sum_{k\geq 0}\frac{1}{1+k}\tm\dfrac{\lambda^k}{k!}e^{-\lambda}\\[1.2em] &=&\dsp\sum_{k\geq 0}\frac{\lambda^k}{(k+1)!}e^{-\lambda}\\[1.4em] &=&\dfrac1{\lambda}\dsp\sum_{k\geq 0}\dfrac{\lambda^{k+1}}{(k+1)!}e^{-\lambda}\\[1.4em] &=&\dfrac{e^{-\lambda}}{\lambda}\left(e^{\lambda}-1\right)\\[1em] &=&\dfrac{1-e^{-\lambda}}{\lambda}. \enar$

Tag:Variables aléatoires discrètes

Autres sujets au hasard:

Voir aussi: