Comparaison de 2 variables géométriques
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires discrètesVariables aléatoires discrètes
Énoncé du sujet
Soit 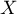 et
et 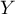 deux variables aléatoires indépendantes suivant des lois
géométriques de paramètres respectifs
deux variables aléatoires indépendantes suivant des lois
géométriques de paramètres respectifs 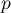 et
et 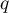 .
.
- Donner, pour
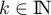 ,
l'expression de
,
l'expression de 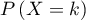 et
et 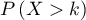 .
.
- Calculer
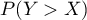 .
.
Correction
Correction
-
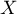 suit une loi géométrique donc
suit une loi géométrique donc
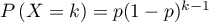 et (c'est du cours aussi, mais il est bon de savoir le (re)démonter):
et (c'est du cours aussi, mais il est bon de savoir le (re)démonter):
![\[\begin{array}{ll}
P\left( X>k\rp&=\dsp\sum_{n>k}P\left( X=n\rp \\[1.4em]
&=\dsp\sum_{n=k+1}^{+\infty}p(1-p)^{n-1}\\
&=p(1-p)^k\dsp\sum_{n=0}^{+\infty}(1-p)^n\\
&=p(1-p)^k\dfrac{1}{1-\lp1-p\right)}\\[1em]
&=(1-p)^k\enar\]](/Generateur-Devoirs/Colles/VAD/CompLoisGeom_c/3.png)
- L'événement
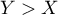 est la réunion des événements disjoints
est la réunion des événements disjoints
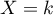 et
et 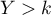 , pour
, pour 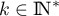 .
On a alors, par indépendance des variables aléatoires
.
On a alors, par indépendance des variables aléatoires 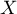 et
et 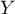 ,
et avec les formules de la question précédente,
,
et avec les formules de la question précédente,
![\[\begin{array}{ll}P(Y>X)
&=\dsp\sum_{k=1}^{+\infty}P\bigl(\left( X=k\rp\cap\left( Y>k\rp\bigr)\\[1.4em]
&=\dsp\sum_{k=1}^{+\infty}P\left( X=k\rp\,P\left( Y>k\rp\\[1.4em]
&=\dsp\sum_{k=1}^{+\infty}p(1-p)^{k-1}(1-q)^k\\[1.4em]
&=\dsp\sum_{k=1}^{+\infty}p(1-q)\Bigl((1-p)(1-q)\Bigr)^{k-1}\\[1em]
&=p(1-q)\dsp\sum_{k=1}^{+\infty}\Bigl((1-p)(1-q)\Bigr)^{k-1}\\
&=p(1-q)\dfrac1{1-(1-p)(1-q)}\\
&=\dfrac{p-pq}{p+q-pq}
\enar\]](/Generateur-Devoirs/Colles/VAD/CompLoisGeom_c/10.png)
Tag:Variables aléatoires discrètes
Autres sujets au hasard:

Voir aussi: