Série alternée: récurrence et convergence
Colle de mathématiques
Sujet de colle de maths:- SuitesSuites
- RécurrenceDémonstration par récuurrence
- SommesSommes des termes d'une suite
- LimiteLimites de suites et de fonctions
Énoncé du sujet
Pour tout entier 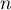 , on pose
, on pose
 .
.
 .
.
- Montrer que, pour tout entier
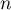 ,
,
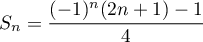 .
.
- Étudier la convergence de
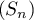 .
.
Correction
Correction
- On peut démontrer ce résultat par récurrence.
Pour
 ,
,  et
et  aussi,
ce qui montre que la propriété est vraie initialement.
aussi,
ce qui montre que la propriété est vraie initialement.
Supposons maintenant que cette propriété soit vraie à un certain rang ,
soit
,
soit 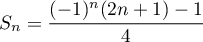 .
.
Au rang suivant, on a alors,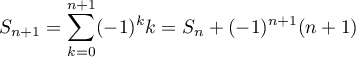 ,
soit, en utilisant l'hypothèse de récurrence,
,
soit, en utilisant l'hypothèse de récurrence,
![\[\begin{array}{ll}
S_{n+1}&\dsp=\dfrac{(-1)^n(2n+1)-1}{4}+(-1)^{n+1}(n+1)\\[1em]
&\dsp=\dfrac{(-1)^{n+1}\left( -2n-1+4(n+1)\rp-1}{4}\\[1em]
&\dsp=\dfrac{(-1)^{n+1}\left( 2n+3\rp-1}{4}\\[1em]
&\dsp=\dfrac{(-1)^{n+1}\left( 2(n+1)+1\rp-1}{4}
\enar\]](/Generateur-Devoirs/Colles/Suites/ex9_c/7.png)
ce qui montre que la propriété est encore vraie au rang suivant.
D'après le principe de récurrence, on peut donc en conclure que la propriété est vraie pour tout entier naturel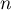 .
.
- D'après le résultat précédent, on a donc que
 diverge vers
diverge vers 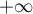 ,
et
,
et 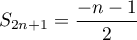 diverge vers
diverge vers  .
.
Ainsi la suite est divergente.
est divergente.
Tags:SuitesRécurrenceSommesLimite
Autres sujets au hasard:
