Variante du théorème de convergence monotone bornée
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
Soit 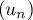 et
et 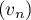 deux suites telles que,
deux suites telles que,
Montrer que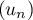 converge.
Que peut-on dire de sa limite ?
converge.
Que peut-on dire de sa limite ?
- pour tout entier
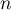 ,
, 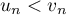
-
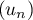 est croissante
est croissante
-
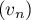 converge vers un réel
converge vers un réel 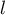 .
.
Montrer que
Correction
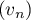 converge vers
converge vers 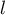 ,
il existe un rang
,
il existe un rang 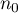 tel que,
pour tout entier
tel que,
pour tout entier  ,
,
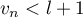 .
.
On a donc, pour tout entier ,
,
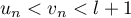 et ainsi
et ainsi 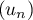 est majorée.
est majorée.
Comme de plus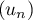 est croissante, on en déduit que
est croissante, on en déduit que
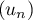 converge vers un réel
converge vers un réel 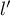 ,
limite dont on peut seulement dire ici que
,
limite dont on peut seulement dire ici que 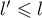 .
.
Correction
CommeOn a donc, pour tout entier
Comme de plus
Tags:SuitesLimite
Autres sujets au hasard:

Voir aussi: