Recherche de fonctions avec une propriété intégrale
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Déterminer l'ensemble des fonction 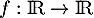 dérivables vérifiant
dérivables vérifiant
![\[\forall (x,y) \in \R^2, \int_{x}^y f(t) dt = \dfrac{y-x}{2} (f(x)+f(y))\]](/Generateur-Devoirs/Colles/Integrale/exR6/2.png)
Correction
On appelle la relation de l'énoncé:
la relation de l'énoncé:
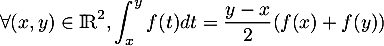
Interprétation graphique de dans le cas où
dans le cas où 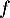 est positive et
est positive et 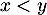 :
l'intégrale est "l'aire sous la courbe", tandis que le membre de droite est l'aire du trapèze hachuré en rouge:
:
l'intégrale est "l'aire sous la courbe", tandis que le membre de droite est l'aire du trapèze hachuré en rouge:
![\[\psset{unit=1cm,arrowsize=8pt}
\begin{pspicture}(-1,-.5)(5,4)
%D\'efinition de la fonction:
\nwc{\f}[1]{
#1 1.6 mul 180 mul 3.14 div sin
#1 div #1 add 1 add 0.8 mul}
%D\'efinition du domaine hachur\'e:
\pscustom{
\psplot{-1.}{3}{\f{x}} \gsave
\psline(3,0)(-1,0)
%\fill[fillstyle=solid,fillcolor=lightgray]
\fill[fillstyle=vlines,hatchsep=10pt,hatchwidth=1.pt,hatchcolor=blue]
\grestore
}
%On retrace la courbe par dessus:
\psplot[linewidth=1pt]{-1.2}{3.2}{\f{x}}
\put(3.1,3.3){$\mathcal{C}_f$}
\psline[linewidth=1pt]{->}(-2,-0.4)(-2,4)
\psline[linewidth=1pt]{->}(-2.5,0)(5,0)
\psline[linewidth=0.5pt,linestyle=dashed]
(-1,-0.2)(!-1 \space \f{-1})(!-2 \space \f{-1})
\rput(-1,-0.5){$x$}\rput[r](-2.2,.8){$f(x)$}
\psline[linewidth=0.5pt,linestyle=dashed]
(3,-0.2)(!3 \space \f{3})(!-2\space\f{3})
\rput(3,-0.5){$y$}\rput[r](-2.2,3){$f(y)$}
% et le trap\`eze
\pscustom{
\psline(!-1\space\f{-1})(!3\space\f{3}) \gsave
\psline(3,0)(-1,0)
%\fill[fillstyle=solid,fillcolor=lightgray]
\fill[fillstyle=hlines,hatchsep=10pt,hatchwidth=1.4pt,hatchcolor=red]
\grestore
}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/6.png)
Assez clairement, graphiquement, si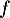 est affine alors les deux domaines, et leurs aires, coïncident. Il s'agit alors de le démontrer, et de montrer qu'on a ainsi toutes les fonctions qui vérifient la relation
est affine alors les deux domaines, et leurs aires, coïncident. Il s'agit alors de le démontrer, et de montrer qu'on a ainsi toutes les fonctions qui vérifient la relation 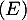 .
.
Condition suffisante: Si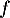 est une fonction affine alors elle est dérivable sur
est une fonction affine alors elle est dérivable sur 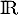 et il existe
et il existe 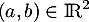 tel que
tel que 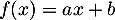 . On calcule alros facilement les 2 membres de
. On calcule alros facilement les 2 membres de 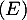 , et on observe bien qu'ils sont égaux à
, et on observe bien qu'ils sont égaux à 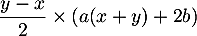 et donc
et donc  vérifie
vérifie  .
.
Réciproquement: Soit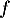 dérivable sur
dérivable sur 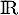 et vérifiant
et vérifiant 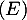 .
.
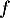 est dérivable donc continue sur
est dérivable donc continue sur 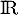 et admet donc des primitives. Soit
et admet donc des primitives. Soit 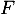 une primitive de
une primitive de 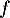 , alors
, alors 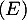 s'écrit
s'écrit
![\[\forall (x,y) \in \R^2, F(y)-F(x) = \dfrac{y-x}{2} (f(x)+f(y))\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/25.png)
Fixons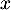 et dérivons par rapport à
et dérivons par rapport à 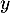 , on obtient par produit de fonctions dérivables :
, on obtient par produit de fonctions dérivables :
![\[\begin{array}{ll}\forall y \in \R, &F'(y)=f(y) = \dfrac{1}{2} (f(x)+f(y)) + \dfrac{y-x}{2} f'(y)\\[1em]
&\iff\dfrac{1}{2} (f(y)-f(x)) = \dfrac{y-x}{2} f'(y)\\[.8em]
&\iff f(y)-f(x) = (y-x) f'(y)
\enar\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/28.png)
En prenant, par exemple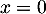 , on obtient la relation
, on obtient la relation
![\[f(y)-f(0)=yf'(y)\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/30.png)
En échangeant les rôles de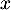 et de
et de 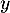 , on obtient cette fois:
, on obtient cette fois:
![\[\forall x \in \R, (f(y)-f(x)) = (y-x) f'(x)\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/33.png)
On prend alors de même que précédemment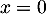 , et on obtient cette fois
, et on obtient cette fois
![\[f(y)-f(0)=yf'(x)\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/35.png)
On obtient donc
![\[f(y)-f(0)=yf'(y)=yf'(x)\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/36.png)
soit
![\[\forall y\in\R, \ y\Bigl( f'(y)-f'(0)\Bigr)=0\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/37.png)
et donc,
![\[\forall y\in\R, \ f'(y)-f'(0)=0 \iff f'(y)=f'(0)\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/38.png)
Ainsi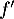 est constante, et donc
est constante, et donc 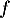 est une fonction affine.
est une fonction affine.
On a donc montré que les fonctions dérivables sur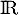 et vérifiant
et vérifiant  sont exactement les fonctions affines.
sont exactement les fonctions affines.
Correction
Oral ENS ULM - 2019On appelle
Interprétation graphique de
![\[\psset{unit=1cm,arrowsize=8pt}
\begin{pspicture}(-1,-.5)(5,4)
%D\'efinition de la fonction:
\nwc{\f}[1]{
#1 1.6 mul 180 mul 3.14 div sin
#1 div #1 add 1 add 0.8 mul}
%D\'efinition du domaine hachur\'e:
\pscustom{
\psplot{-1.}{3}{\f{x}} \gsave
\psline(3,0)(-1,0)
%\fill[fillstyle=solid,fillcolor=lightgray]
\fill[fillstyle=vlines,hatchsep=10pt,hatchwidth=1.pt,hatchcolor=blue]
\grestore
}
%On retrace la courbe par dessus:
\psplot[linewidth=1pt]{-1.2}{3.2}{\f{x}}
\put(3.1,3.3){$\mathcal{C}_f$}
\psline[linewidth=1pt]{->}(-2,-0.4)(-2,4)
\psline[linewidth=1pt]{->}(-2.5,0)(5,0)
\psline[linewidth=0.5pt,linestyle=dashed]
(-1,-0.2)(!-1 \space \f{-1})(!-2 \space \f{-1})
\rput(-1,-0.5){$x$}\rput[r](-2.2,.8){$f(x)$}
\psline[linewidth=0.5pt,linestyle=dashed]
(3,-0.2)(!3 \space \f{3})(!-2\space\f{3})
\rput(3,-0.5){$y$}\rput[r](-2.2,3){$f(y)$}
% et le trap\`eze
\pscustom{
\psline(!-1\space\f{-1})(!3\space\f{3}) \gsave
\psline(3,0)(-1,0)
%\fill[fillstyle=solid,fillcolor=lightgray]
\fill[fillstyle=hlines,hatchsep=10pt,hatchwidth=1.4pt,hatchcolor=red]
\grestore
}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/6.png)
Assez clairement, graphiquement, si
Condition suffisante: Si
Réciproquement: Soit
Fixons
![\[\begin{array}{ll}\forall y \in \R, &F'(y)=f(y) = \dfrac{1}{2} (f(x)+f(y)) + \dfrac{y-x}{2} f'(y)\\[1em]
&\iff\dfrac{1}{2} (f(y)-f(x)) = \dfrac{y-x}{2} f'(y)\\[.8em]
&\iff f(y)-f(x) = (y-x) f'(y)
\enar\]](/Generateur-Devoirs/Colles/Integrale/exR6_c/28.png)
En prenant, par exemple
En échangeant les rôles de
On prend alors de même que précédemment
On obtient donc
soit
et donc,
Ainsi
On a donc montré que les fonctions dérivables sur
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: