Calcul d'intégrale avec changement de variable


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

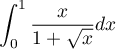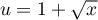Calculer l'intégrale $\dsp\int_0^1\dfrac{x}{1+\sqrt{x}}dx$ en utilisant le changement de variable $u=1+\sqrt{x}$.


Correction

Correction

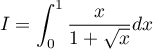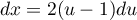Soit $I=\dsp\int_0^1\dfrac{x}{1+\sqrt{x}}dx$ et le changement de variable $u=1+\sqrt{x}\iff x=(u-1)^2$ et $dx=2(u-1)du$, et alors (en n'oubliant pas les bornes)
\[\begin{array}{ll} I=&2\dsp\int_1^2\dfrac{(u-1)^2}{u}(u-1)\,du\\[1.2em] &=2\dsp\int_1^2\dfrac{(u-1)^3}{u}\,du\\[1.2em] &=2\dsp\int_1^2\dfrac{u^3-3u^2+3u-1}{u}\,du\\[1.2em] &=2\dsp\int_1^2u^2du-6\int_1^2u\,du+6\int_1^2du-2\int_1^2\dfrac1udu\\[1.2em] &=\dfrac23\Bigl[ u^3\Bigr]_1^2-3\Bigl[ u^2\Bigr]_1^2+6\Bigl[ u\Bigr]_1^2-2\Bigl[\ln u\Bigr]_1^2\\[1.2em] &=\dfrac23\tm7-3\tm3+3\tm1-2\ln2 \\[.8em] &=\dfrac53-\ln2 \enar\]



Tag:Intégrale

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0