Recherche de fonctions avec une propriété intégrale
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Déterminer les fonction  , continues et telles que
, continues et telles que
 ,
, 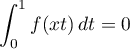 .
.
Correction
 , pour
, pour  :
:
![\[\int_0^1 f(xt)\,dt=\dfrac1x\int_0^x f(u)\,du\]](/Generateur-Devoirs/Colles/Integrale/exR5_c/3.png)
ce qui signifie que la valeur moyenne de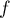 sur
sur ![$[0;x]$](/Generateur-Devoirs/Colles/Integrale/exR5_c/5.png) , pour tout
, pour tout 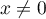 est nulle, et qui laisse bien penser que
est nulle, et qui laisse bien penser que 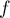 est identiquement nulle.
est identiquement nulle.
Plus rigoureusement, on reconnaît la primitive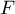 de
de 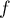 qui s'annule en 0:
qui s'annule en 0:
![\[\int_0^xf(u)du=F(x)=0\]](/Generateur-Devoirs/Colles/Integrale/exR5_c/10.png)
Ainsi, cette primitive est la fonction nulle, et donc aussi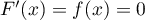 , pour
, pour 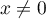 .
.
Enfin, comme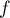 est continue sur
est continue sur 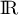 on a nécessairement
on a nécessairement 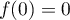 et donc
et donc  est identiquement nulle sur
est identiquement nulle sur 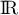 .
.
Correction
On est assez fortement incité à faire le changement de variablece qui signifie que la valeur moyenne de
Plus rigoureusement, on reconnaît la primitive
Ainsi, cette primitive est la fonction nulle, et donc aussi
Enfin, comme
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: