Calculer l'intégrale trigonométrique avec changement de variable
Colle de mathématiques
Sujet de colle de maths:- IntégraleIntégrale
Énoncé du sujet
Calculer
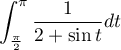 à l'aide du changement de variables
à l'aide du changement de variables
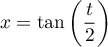
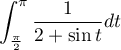 à l'aide du changement de variables
à l'aide du changement de variables
Correction
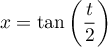 alors d'une part,
alors d'une part,
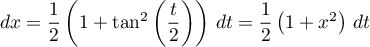
et, d'autre part il faut exprimer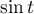 en fonction de
en fonction de 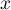 .
Il faut clairement faire appel à l'angle moitié:
.
Il faut clairement faire appel à l'angle moitié:
![\[\begin{array}{ll}\sin t&=2\sin\dfrac{t}{2}\cos\dfrac{t}{2} \\[.8em]
&=2\tan\dfrac{t}{2}\cos^2\dfrac{t}{2}\\[.8em]
&=2x\cos^2\dfrac{t}{2}
\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/5.png)
Enfin, pour exprimer ce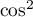 , on a aussi
, on a aussi
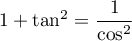 , soit ici
, soit ici
![\[\begin{array}{ll}\sin t&=2x\dfrac1{1+\tan^2\dfrac{t}{2}}\\[.8em]
&=\dfrac{2x}{1+x^2}\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/8.png)
On a alors, en n'oubliant pas les bornes de l'intégrale,
![\[\begin{array}{ll}I&=\dsp\int_{\frac\pi2}^\pi\dfrac1{2+\sin t}dt\\[.8em]
&=\dsp\int_1^{+\infty}\dfrac{2dx}{\lp1+x^2\rp\lp2+\dfrac{2x}{1+x^2}\rp}\\[.8em]
&=\dsp\int_1^{+\infty}\dfrac{dx}{x^2+x+1}\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/9.png)
Il reste maintenant à calculer l'intégrale de cette fonction rationnelle: forme canonique et arctangente:
![\[\begin{array}{ll}I&=\dsp\int_1^{+\infty}\dfrac{dx}{\left( x+\frac12\rp^2+\frac34}\\[1em]
&=\dsp\int_1^{+\infty}\dfrac{dx}{\dfrac34\Bigl[\left( \frac{2}{\sqrt3}\left( x+\frac12\rp\rp^2+1\Bigr]}
\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/10.png)
puis, en posant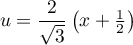 donc
donc 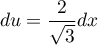 ,
,
![\[\begin{array}{ll}I&=\dsp\dfrac43\int_{\sqrt3}^{+\infty}\dfrac{\frac{\sqrt3}{2}du}{u^2+1}\\[1em]
&=\dfrac2{\sqrt3}\Bigl[\,\arctan u\,\Bigr]_{\sqrt3}^{+\infty} \\[1em]
&=\dfrac2{\sqrt3}\Bigl[\dfrac\pi2-\dfrac\pi3\Bigr]\\[1em]
&=\dfrac\pi{3\sqrt3}\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/13.png)
Correction
Soit doncet, d'autre part il faut exprimer
![\[\begin{array}{ll}\sin t&=2\sin\dfrac{t}{2}\cos\dfrac{t}{2} \\[.8em]
&=2\tan\dfrac{t}{2}\cos^2\dfrac{t}{2}\\[.8em]
&=2x\cos^2\dfrac{t}{2}
\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/5.png)
Enfin, pour exprimer ce
![\[\begin{array}{ll}\sin t&=2x\dfrac1{1+\tan^2\dfrac{t}{2}}\\[.8em]
&=\dfrac{2x}{1+x^2}\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/8.png)
On a alors, en n'oubliant pas les bornes de l'intégrale,
![\[\begin{array}{ll}I&=\dsp\int_{\frac\pi2}^\pi\dfrac1{2+\sin t}dt\\[.8em]
&=\dsp\int_1^{+\infty}\dfrac{2dx}{\lp1+x^2\rp\lp2+\dfrac{2x}{1+x^2}\rp}\\[.8em]
&=\dsp\int_1^{+\infty}\dfrac{dx}{x^2+x+1}\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/9.png)
Il reste maintenant à calculer l'intégrale de cette fonction rationnelle: forme canonique et arctangente:
![\[\begin{array}{ll}I&=\dsp\int_1^{+\infty}\dfrac{dx}{\left( x+\frac12\rp^2+\frac34}\\[1em]
&=\dsp\int_1^{+\infty}\dfrac{dx}{\dfrac34\Bigl[\left( \frac{2}{\sqrt3}\left( x+\frac12\rp\rp^2+1\Bigr]}
\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/10.png)
puis, en posant
![\[\begin{array}{ll}I&=\dsp\dfrac43\int_{\sqrt3}^{+\infty}\dfrac{\frac{\sqrt3}{2}du}{u^2+1}\\[1em]
&=\dfrac2{\sqrt3}\Bigl[\,\arctan u\,\Bigr]_{\sqrt3}^{+\infty} \\[1em]
&=\dfrac2{\sqrt3}\Bigl[\dfrac\pi2-\dfrac\pi3\Bigr]\\[1em]
&=\dfrac\pi{3\sqrt3}\enar\]](/Generateur-Devoirs/Colles/Integrale/exC8_c/13.png)
Tag:Intégrale
Autres sujets au hasard:

Voir aussi: