Rayon de convergence


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

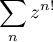
Déterminer le rayon de convergence de la série entière $\dsp\sum_n z^{n!}$


Correction

Correction

Pour $|z|<1$, on remarque que $|z|^{n!}\leq |z|^n$ et donc la série est convergente. Pour $|z|\geq 1$, le terme général de la série ne tend pas vers 0 et la série est donc grossièrement divergente. On en déduit que le rayon de convergence de la série entière est 1.


Tag:Séries entières

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0