Développement en série entière d'une fonction
Colle de mathématiques
Sujet de colle de maths:- Séries entièresSéries entières
Énoncé du sujet
Développer en série entière au voisinage de 0 la fonction 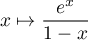 .
Préciser le rayon de convergence de la série entière obtenue.
.
Préciser le rayon de convergence de la série entière obtenue.
Correction
![\[e^x=\sum_{n=0}^{+\infty}\frac{x^n}{n!}\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/1.png)
et
![\[\frac{1}{1-x}=\sum_{n=0}^{+\infty}x^n\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/2.png)
La deuxième série ayant pour rayon de convergence 1, on en déduit que pour , on a
, on a
![\[\frac{e^x}{1-x}=\sum_{n=0}^{+\infty}a_n x^n\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/4.png)
avec
![\[a_n=\sum_{k=0}^n\frac{1}{k!}\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/5.png)
La série converge pour (règle du produit de Cauchy), et comme
(règle du produit de Cauchy), et comme 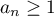 , le rayon de
convergence de la série obtenue est exactement égal à 1 puisque, pour
, le rayon de
convergence de la série obtenue est exactement égal à 1 puisque, pour 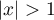 , la série
, la série 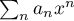 diverge grossièrement puisque son terme général ne tend pas vers zéro.
diverge grossièrement puisque son terme général ne tend pas vers zéro.
Correction
On réalise le produit de Cauchy des deux séries :![\[e^x=\sum_{n=0}^{+\infty}\frac{x^n}{n!}\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/1.png)
et
![\[\frac{1}{1-x}=\sum_{n=0}^{+\infty}x^n\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/2.png)
La deuxième série ayant pour rayon de convergence 1, on en déduit que pour
![\[\frac{e^x}{1-x}=\sum_{n=0}^{+\infty}a_n x^n\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/4.png)
avec
![\[a_n=\sum_{k=0}^n\frac{1}{k!}\]](/Generateur-Devoirs/Colles/SeriesEnt/exDLSE4_c/5.png)
La série converge pour
Tag:Séries entières
Autres sujets au hasard:

Voir aussi: