Racine carrée d'une loi exponentielle

Colle de mathématiques

Sujet de colle de maths:

Variables aléatoires continuesVariables aléatoires continues

Énoncé du sujet

Soit 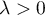$\lambda>0$ et

$f:\R\to\R, \, x\mapsto\la\begin{array}{cl} 0 &\text{si } x\leqslant0 \\ \lambda e^{-\lambda x} &\text{sinon}\enar\right.$

Vérifier que est une densité de probabailité d'une variable aléatoire.
Soit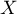 admettant pour densité.
Montrer que et existent et les calculer.
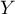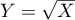On définit par $Y=\sqrt{X}$ . Déterminer une densité de .
Montrer que 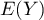et 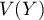existent et les calculer.

Correction

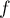est clairement positive et continue, sauf en 0, et

$\begin{array}{ll}\dsp\int_{-\infty}^{+\infty}f(x)dx &=\dsp\lambda\int_0^{+\infty}e^{-\lambda x}dx\\ &=\lambda\left[ -\dfrac1\lambda e^{-\lambda x}\rb_0^{+\infty} =1\enar$

ce qui finit de montrer que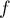 est une densité de variable aléatoire.
$E(X)=\lambda\int_0^{+\infty}xe^{-\lambda x}dx$

Comme

$\dsp\lim_{x\to+\infty}x^2\left( xe^{-\lambda x}\rp=0$

et d'après le critère de Riemann, cette intégrale converge bien en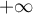 $+\infty$ , et, en intégrant par parties,

$\begin{array}{ll}E(X)&=\dsp\lambda\lb-\dfrac{x}\lambda e^{-\lambda x}\rb_0^{+\infty} +\int_0^{+\infty}e^{-\lambda x}dx\\ &=0+\lb-\dfrac1\lambda e^{-\lambda x}\rb_0^{+\infty}\\ &=\dfrac1\lambda\enar$

et de même (ou en ayant reconnu la loi exponentielle)

$V(X)=\dfrac1{\lambda^2}$
$\begin{array}{ll}F_Y(x)&=P(Y\leqslant x)\\ &=P\lp\sqrt{X}\leqslant x\rp\\ &=P\left( X\leqslant x^2\rp\\ &=F_X\left( x^2\rp\enar$

d'où

$F_Y(x)=\la\begin{array}{cl}0&\text{si} x\leqslant0\\ F_X\left( x^2\rp=&\text{sinon}\enar\right.$

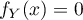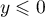et donc, la densité, pour $y\leqslant0$ et, pour 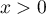en dérivant

$f_Y(x)=2\lambda xF'_X(x^2)=2xe^{-\lambda x^2}$
$E(Y)=\int_{-\infty}^{+\infty}yf_Y(y)dy =2\lambda \int_0^{+\infty}y^2e^{-\lambda y^2}dy$

et, en intégrant par parties

$\begin{array}{ll}\dsp\int_0^{+\infty}&y^2e^{-\lambda y^2}dy =\dsp\int_0^{+\infty} y\times y e^{-\lambda y^2}dy\\[1em] &=\dsp\left[ y\tm\dfrac{-1}{2\lambda} e^{-\lambda y^2}\rb_0^{+\infty} +\dfrac1{2\lambda}\int_0^{+\infty} e^{-\lambda y^2}dy \enar$

La partie intégrée est nulle, et la dernière intégrale se calcule en se ramenant à la loi normale, en posant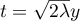 $t=\sqrt{2\lambda}y$ , soit

$\int_0^{+\infty}e^{-\lambda y^2}dy =\dfrac1{\sqrt{2\lambda}}\int_0^{+\infty} e^{-t^2/2}dt$

car pour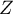 qui suit la loi normale centrée réduite,

$\begin{array}{ll}&P(Z\geqslant0)=\dsp\int_0^{+\infty}\dfrac1{\sqrt{2\pi}}e^{-t^2/2}dt =\dfrac12\\ &\implies\displaystyle \int_0^{+\infty}e^{-t^2/2}dt =\dfrac{\sqrt{2\pi}}2=\sqrt{\dfrac\pi2} \enar$

d'où

$E(Y)=2\lambda\int_0^{+\infty}y^2e^{-\lambda y^2}dy =\dfrac1{\sqrt{2\lambda}}\sqrt{\dfrac\pi2} =\dfrac12\sqrt{\dfrac\pi\lambda}$

On a ensuite $E(Y^2)=E(X)=\dfrac1\lambda$ , et donc

$V(Y)=E\left( Y^2\rp-\left( E(Y)\rp^2=\dfrac1\lambda-\dfrac\pi{4\lambda} =\dfrac{4-\pi}{4\lambda}$

Tag:Variables aléatoires continues

Autres sujets au hasard: