Intégrale et loi normale

Colle de mathématiques

Sujet de colle de maths:

Variables aléatoires continuesVariables aléatoires continues

Énoncé du sujet

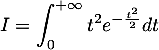
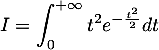
Soit $I=\dsp\int_0^{+\infty}t^2e^{-\frac{t^2}2}dt$

Montrer que l'intégrale est convergente, puis la calculer.
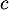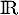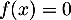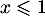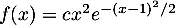Pour quelle valeur du réel , la fonction définie sur $\R$ par si $x\leqslant1$ et $f(x)=cx^2e^{-(x-1)^2/2}$ sinon est-elle une densité de probabilité ?

Correction

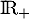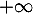La fonction à intégrer est clairement continue sur $\R_+$ , donc l'intégrale est seulement impropre en $+\infty$ .
On a, par croissances comparées,

$\lim_{t\to+\infty}t^2.t^2e^{-\frac{(t-1)^2}2}=0$

ce qui signfie que

$t^2e^{-\frac{(t-1)^2}2} = o\lp\dfrac1{t^2}\rp$

avec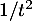 intégrable en 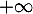$+\infty$ (intégrale de Riemann), et donc l'intégrale converge bien.

On intègre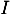 par parties:

$\begin{array}{ll} I&=\dsp\int_0^{+\infty}t\times te^{-\frac{t^2}2}dt\\ &=\dsp\left[ -te^{-\frac{t^2}2}\rb_0^{+\infty}-\int_0^{+\infty}-e^{-\frac{t^2}2}dt\\[1em] &= \qquad 0\hspace{3em}+ \ \dsp\int_0^{+\infty}e^{-\frac{t^2}2}dt \enar$

Cette dernière intégrale nous rappele la loi normale, dont la densité est

$\varphi(t)=\dfrac1{\sqrt{2\pi}}e^{-\frac{t^2}2}$

et, comme il s'agit de la densité d'une loi de probabilité,

$\int_{-\infty}^{+\infty}\varphi(t)dt=1$

et donc, par parité de la fonction à intégrée:

$\int_0^{+\infty}e^{-\frac{t^2}2}(t)dt=\dfrac{\sqrt{2\pi}}2$

Ainsi,

$I=\dfrac{\sqrt{2\pi}}2$
La fonction 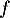est clairement continue sur 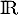$\R$ , et positive.
Il reste à déterminer pour

$\int_{-\infty}^{+\infty}f(x)dx=1$

soit

$c\int_1^{+\infty}x^2e^{-\frac{(x-1)^2}2}=1$

On appelle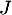 l'intégrale précédente.
Pour se ramener à la question précédente, on fait le changement de variable affine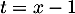 , et alors

$\begin{array}{ll}J=&\dsp\int_1^{+\infty}x^2e^{-\frac{(x-1)^2}2}\\ &=\dsp\int_0^{+\infty}(t+1)^2e^{-\frac{t^2}2}dt\enar$

En développant on a alors trois intégrales à calculer:

$J=\dsp\int_0^{+\infty}t^2e^{-\frac{t^2}2}dt + 2\int_0^{+\infty}te^{-\frac{t^2}2}dt +\int_0^{+\infty}e^{-\frac{t^2}2}dt$

La première est celle de la question précédente.
La deuxième s'intègre directement, comme à la question précédente:

$\int_0^{+\infty}te^{-\frac{t^2}2}dt=\left[ -e^{-\frac{t^2}2}\rb_0^{+\infty}=1$

La troisième a été calculé à la question précédente et vaut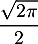 $\dfrac{\sqrt{2\pi}}2$ .

En résumé, on a donc

$\begin{array}{ll}J&=\dfrac{\sqrt{2\pi}}2+2\tm1+\dfrac{\sqrt{2\pi}}2+\dfrac{\sqrt{2}}2\\ &=2+\sqrt{2}\enar$

Tag:Variables aléatoires continues

Autres sujets au hasard:

Voir aussi: