Fonction de répartition et nouvelle densité
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit 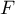 une fonction de répartition d'une variable aléatoire
à densité.
une fonction de répartition d'une variable aléatoire
à densité.
- Montrer que
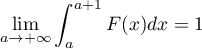 et que
et que 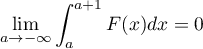
- Montrer que la fonction
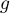 définie sur
définie sur 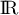 par
l'expression
par
l'expression
![\[g(x)=F(x+1)-F(x)\]](/Generateur-Devoirs/Colles/VAC/prrepdst/6.png)
est une densité de probabilité.
Correction
Correction
- On sait que
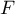 est croissante sur
est croissante sur 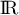 , et que
, et que
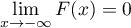 et
et 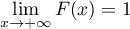 .
.
On utilise la croissance de la fonction pour l'encadrer:
et donc, en intégrant,![\[\forall x\in[a;a+1], \quad
F(a)\leq F(x)\leq F(a+1)\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/5.png)
![\[\int_a^{a+1}F(a)dx\leq\int_a^{a+1}F(x)dx\leq\int_a^{a+1}F(a+1)dx\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/6.png)
soit
![\[F(a)\leq\int_a^{a+1}F(x)dx\leq F(a+1)\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/7.png)
On a de plus par hypothèse sur la limite de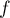 ,
,
![\[\lim_{a\to+\infty}F(a)=\lim_{a\to+\infty}F(a+1)=1\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/9.png)
et donc, par le théorème des gendarmes,
![\[\lim_{a\to+\infty}\int_a^{a+1}F(x)dx=1\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/10.png)
À partir du même encadrement, et comme
![\[\lim_{a\to-\infty}F(a)=\lim_{a\to-\infty}F(a+1)=0\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/11.png)
on a alors aussi
![\[\lim_{a\to-\infty}\int_a^{a+1}F(x)dx=0\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/12.png)
- Il faut vérifier trois points:
-
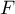 est continue sur
est continue sur 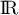 en tant que fonction de répartition
d'une variable à densité, et donc
en tant que fonction de répartition
d'une variable à densité, et donc 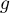 est continue
comme composée de fonctions continues.
est continue
comme composée de fonctions continues.
-
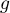 est positive car
est positive car 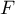 étant une fonction de répartition elle
est en particulier croissante, et donc, pour tout réel
étant une fonction de répartition elle
est en particulier croissante, et donc, pour tout réel 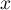
![\[F(x+1)\geq F(x) \Longrightarrow g(x)\geq0\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/19.png)
- il faut enfin que
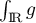 existe (converge) et soit égale à 1.
existe (converge) et soit égale à 1.
Soit donc deux réels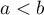 , alors
, alors
![\[\begin{array}{ll}\dsp\int_a^bg(x)dx
&=\dsp\int_a^b\bigl(F(x+1)-F(x)\bigr)dx\\
&=\dsp\int_a^b F(x+1)dx-\int_a^b F(x)dx\enar\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/22.png)
et en effectuant le changement de variable affine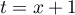 dans la première intégrale:
dans la première intégrale:
![\[\int_a^bg(x)dx=\int_{a+1}^{b+1}F(t)dt-\int_a^bF(x)dx\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/24.png)
puis, par la relation de Chasles,
![\[\int_a^bg(x)dx=\int_b^{b+1}F(x)dx-\int_a^{a+1}F(x)dx\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/25.png)
Enfin, d'après la première question on trouve que, lorsque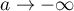 et
et 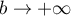 ,
,
![\[\int_{-\infty}^{+\infty}g(x)dx=1-0=1\]](/Generateur-Devoirs/Colles/VAC/prrepdst_c/28.png)
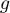 définie bien une densité de probabilité.
définie bien une densité de probabilité.
-
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: