Calcul d'intégrales grâce à la loi normale
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Rappeler la fonction densité d'une variable aléatoire de loi normale
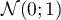 .
.
En déduire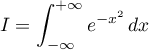 .
Calculer ensuite
.
Calculer ensuite
 .
.
En déduire
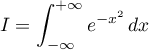 .
Calculer ensuite
.
Calculer ensuite
 .
.
Correction
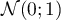 est
est
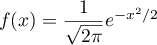 , qui vérifie en particulier
, qui vérifie en particulier
![\[\int_{-\infty}^{+\infty}f(x)\,dx=
\int_{-\infty}^{+\infty}\dfrac1{\sqrt{2\pi}}e^{-x^2/2}\,dx=1\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/3.png)
On a, en particulier
![\[\int_{-\infty}^{+\infty}e^{-x^2/2}\,dx=\sqrt{2\pi}\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/4.png)
puis, avec le changement de variable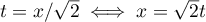
![\[\int_{-\infty}^{+\infty}e^{-x^2/2}\,dx
=\int_{-\infty}^{+\infty}e^{-t^2}\,\sqrt2dt\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/6.png)
et on trouve finalement
![\[\int_{-\infty}^{+\infty}e^{-t^2}\,dt=\dfrac1{\sqrt2}\sqrt{2\pi}=\sqrt{\pi}\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/7.png)
On se ramène au cas précédent en utiisant la forme canonique
![\[-x^2+2x+1=-(x-1)^2+2\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/8.png)
d'où
![\[\begin{array}{ll}\dsp\int_{-\infty}^{+\infty}e^{-x^2+2x+1}\,dx
&=\dsp\int_{-\infty}^{+\infty}e^{-(x-1)^2+2}\,dx\\[1.2em]
&=e^2\dsp\int_{-\infty}^{+\infty}e^{-(x-1)^2}\,dx\enar\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/9.png)
puis, avec le changement de variable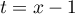 , et le résultat précédent,
, et le résultat précédent,
![\[\int_{-\infty}^{+\infty}e^{-(x-1)^2}\,dx
=\int_{-\infty}^{+\infty}e^{-t^2}\,dt=\sqrt\pi\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/11.png)
et ainsi, finalement,
![\[\int_{-\infty}^{+\infty}e^{-(x-1)^2+2}\,dx
=e^2\sqrt\pi\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/12.png)
Correction
La fonction densité d'une loi normale centrée réduiteOn a, en particulier
puis, avec le changement de variable
et on trouve finalement
On se ramène au cas précédent en utiisant la forme canonique
d'où
![\[\begin{array}{ll}\dsp\int_{-\infty}^{+\infty}e^{-x^2+2x+1}\,dx
&=\dsp\int_{-\infty}^{+\infty}e^{-(x-1)^2+2}\,dx\\[1.2em]
&=e^2\dsp\int_{-\infty}^{+\infty}e^{-(x-1)^2}\,dx\enar\]](/Generateur-Devoirs/Colles/VAC/ints-loi-normale_c/9.png)
puis, avec le changement de variable
et ainsi, finalement,
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: