Projections orthogonales
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
- ProjecteursProjecteurs dans des espaces vectoriels
Énoncé du sujet
Soit 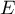 un espace vectoriel euclidien, et
un espace vectoriel euclidien, et 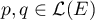 deux projecteurs orthogonaux.
deux projecteurs orthogonaux.
- Montrer que, pour tout
 , on a
, on a  .
.
-
Montrer que
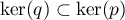 si et seulement si, pour tout
si et seulement si, pour tout 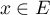 ,
, 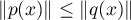
Correction
Correction
- On écrit la décomposition orthognale
sur
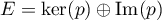 :
:
![\[x=p(x)+(x-p(x))\]](/Generateur-Devoirs/Colles/EspaceEuclidien/projortho_c/2.png)
avec, par le théorème de Pythagore,
![\[\|x\|^2=\|p(x)\|^2+\|x-p(x)\|^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/projortho_c/3.png)
d'où le résultat
![\[\|p(x)\|\leqslant\|x\|\]](/Generateur-Devoirs/Colles/EspaceEuclidien/projortho_c/4.png)
- Supposons que pour tout
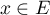 ,
, 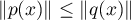 .
.
Soit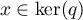 , c'est-à-dire
, c'est-à-dire 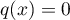 et
alors on a
et
alors on a
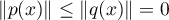 , d'où
, d'où 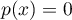 et donc
et donc
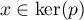 .
.
On vient donc de montrer que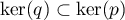 .
.
Réciproquement, supposons maintenant que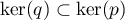 .
.
Soit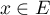 qu'on décompose suivant la projection
qu'on décompose suivant la projection 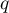 ,
soit
,
soit
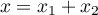 avec
avec 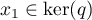 et
et 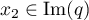 alors
alors
![\[q(x)=x_2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/projortho_c/19.png)
et
![\[p(x)=p(x_1)+p(x_2)=p(x_2)\]](/Generateur-Devoirs/Colles/EspaceEuclidien/projortho_c/20.png)
car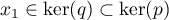 .
.
Or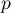 est une projection orthogonale, donc, d'après la question précédente,
est une projection orthogonale, donc, d'après la question précédente,
![\[\|p(x_2)\|\leqslant\|x_2\|\]](/Generateur-Devoirs/Colles/EspaceEuclidien/projortho_c/23.png)
d'où ici
![\[\|p(x)\|=\|p(x_2)\|\leqslant\|x_2\|=\|q(x)\|\]](/Generateur-Devoirs/Colles/EspaceEuclidien/projortho_c/24.png)
Tags:Espaces euclidiensProjecteurs
Autres sujets au hasard:

Voir aussi: