Symétrie dans le plan (bis)
Colle de mathématiques
Sujet de colle de maths:- ProjecteursProjecteurs dans des espaces vectoriels
- Applications linéairesApplications linéaires
Énoncé du sujet
L'application 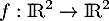 ,
, 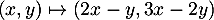 est-elle une projection ou une symétrie ? Préciser ses caractéristiques.
est-elle une projection ou une symétrie ? Préciser ses caractéristiques.
Correction
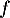 est tout d'abord une application linéaire puisque pour
est tout d'abord une application linéaire puisque pour 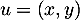 et
et 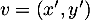 dans
dans 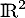 , et
, et 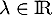 , on a
, on a 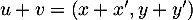 et:
et:
![\[\begin{array}{lcl}
f(u+v)&=&\Bigr( 2(x+x')-(y+y'), 3(x+x')-2(y+y')\Bigl)\\[.5em]
&=&\big(2x-y+2x'-y', 3x-2y+3x'-2y'\bigr)\\[.4em]
&=&(2x-y, 3x-2y) + (2x'-y',3x'-2y')\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/7.png)
et avec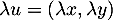 ,
,
![\[\begin{array}{lcl}
f(\lambda u)&=&(2\lambda x-\lambda y,3\lambda x-2\lambda y)\\[.4em]
&=&\lambda(2x-y,3x-2y)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/9.png)
Ainsi,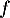 est un endomorphisme de
est un endomorphisme de 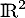 .
.
Un projecteur et une symétrie sont caractérisés par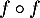 :
soit
:
soit 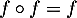 et alors
et alors 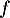 est un projecteur, soit
est un projecteur, soit 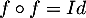 et
et 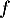 est une symétrie.
est une symétrie.
Ici, pour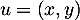 , on a
, on a 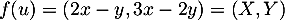 puis,
puis,
![\[\begin{array}{ll}f^2(u)&=f(f(u))\\[.3em]
&=f(X,Y)\\[.3em]
&=(2X-Y,3X-2Y)\\[.3em]
&=\Bigl(2(2x-y)-(3x-2y),3(2x-y)-2(3x-2y)\Bigr)\\[.3em]
&=(x,y)\\[.3em]
&=f(u)\enar\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/19.png)
ce qui montre donc que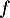 est donc une symétrie.
est donc une symétrie.
L'axe de la symétrie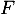 est invariant par
est invariant par 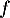 ,
soit
,
soit 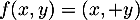 donc
donc
![\[\la\begin{array}{rcl}2x-\ y&=&x\\3x-2y&=&y\enar\right.\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/24.png)
ce qui nous donne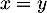 , équation de la droite dans le plan
, équation de la droite dans le plan 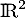 qui est l'axe de la symétrie, ou encore, en d'autres termes
qui est l'axe de la symétrie, ou encore, en d'autres termes 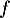 est une symétrie d'axe
est une symétrie d'axe 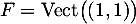 .
.
La direction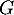 de la symétrie est donnée par la relation
de la symétrie est donnée par la relation 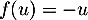 , soit, avec
, soit, avec 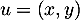 ,
,
![\[\la\begin{array}{rcl}2x-\ y&=&-x\\3x-2y&=&-y\enar\right.\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/32.png)
qui donne cette fois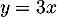 , et donc
, et donc 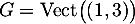 .
.
Correction
![\[\begin{array}{lcl}
f(u+v)&=&\Bigr( 2(x+x')-(y+y'), 3(x+x')-2(y+y')\Bigl)\\[.5em]
&=&\big(2x-y+2x'-y', 3x-2y+3x'-2y'\bigr)\\[.4em]
&=&(2x-y, 3x-2y) + (2x'-y',3x'-2y')\\[.4em]
&=&f(u)+f(v).
\enar\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/7.png)
et avec
![\[\begin{array}{lcl}
f(\lambda u)&=&(2\lambda x-\lambda y,3\lambda x-2\lambda y)\\[.4em]
&=&\lambda(2x-y,3x-2y)\\[.4em]
&=&\lambda f(u).
\enar\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/9.png)
Ainsi,
Un projecteur et une symétrie sont caractérisés par
Ici, pour
![\[\begin{array}{ll}f^2(u)&=f(f(u))\\[.3em]
&=f(X,Y)\\[.3em]
&=(2X-Y,3X-2Y)\\[.3em]
&=\Bigl(2(2x-y)-(3x-2y),3(2x-y)-2(3x-2y)\Bigr)\\[.3em]
&=(x,y)\\[.3em]
&=f(u)\enar\]](/Generateur-Devoirs/Colles/Applin/exSplan2_c/19.png)
ce qui montre donc que
L'axe de la symétrie
ce qui nous donne
La direction
qui donne cette fois
Tags:ProjecteursApplications linéaires
Autres sujets au hasard:

Voir aussi: