Endomorphisme qui conserve l'orthogonalité
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
Énoncé du sujet
Soit 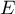 un espace euclidien de dimension
un espace euclidien de dimension 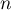 ,
muni du produit scalaire
,
muni du produit scalaire 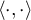 et
de la norme associée
et
de la norme associée  .
.
Soit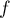 un endomorphisme de
un endomorphisme de 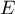 qui vérifie
qui vérifie
![\[\forall (x,y)\in E^2\, , \, \langle x , y \rangle=0
\implies \langle f(x) , f(y) \rangle=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho/7.png)
Soit
- Montrer que si
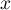 et
et 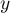 sont des vecteurs de même norme, alors
sont des vecteurs de même norme, alors
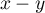 et
et 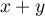 sont orthogonaux.
sont orthogonaux.
- Montrer qu'il existe un réel positif
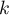 tel que,
pour tout vecteur unitaire
tel que,
pour tout vecteur unitaire 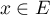 , on a
, on a 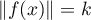 .
.
- Montrer que, pour tout
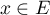 ,
, 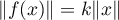 .
.
Correction
Correction
- On a, en utilisant la bilinéarité et la symétrie du produit scalaire
![\[\begin{array}{ll}\langle x-y , x+y\rangle
&= \|x\|^2+\langle x,y\rangle -\langle y,x\rangle - \|y\|^2\\
&=\|x\|^2-\|y\|^2\\
&=0\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho_c/1.png)
pour des vecteurs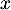 et
et 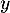 de même norme.
de même norme.
- Soit un vecteur unitaire
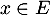 , c'est-à-dire que
, c'est-à-dire que
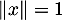 , et posons
, et posons 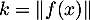 .
.
Soit alors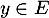 un autre vecteur unitaire, et montrons que
un autre vecteur unitaire, et montrons que
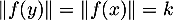 .
.
Comme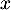 et
et 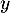 sont tous les deux unitaires, ils ont en particulier
la même norme, et donc, d'après la question précédente,
sont tous les deux unitaires, ils ont en particulier
la même norme, et donc, d'après la question précédente,
![\[\langle x-y , x+y\rangle=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho_c/11.png)
et donc, par hypothèse sur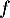 ,
,
![\[\langle f(x-y) , f(x+y)\rangle=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho_c/13.png)
En utilisant alors la linéarité de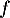 et la bilinéarité du produit scalaire,
on obtient
et la bilinéarité du produit scalaire,
on obtient
![\[\begin{array}{ll}
0&=\langle f(x-y) , f(x+y)\rangle\\
&=\|f(x)\|^2+\langle f(x) , f(y)\rangle
-\langle f(y) , f(x)\rangle
-\|f(y)\|^2
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho_c/15.png)
et donc, par symétrie du produit scalaire,
![\[\|f(x)\|=\|f(y)\|=k\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho_c/16.png)
- Pour tout vecteur unitaire
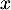 on a donc
on a donc 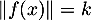 .
.
Soit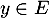 . Si
. Si 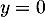 , on a directement
, on a directement 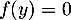 donc
donc
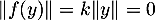 .
.
Pour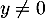 , on se ramène au cas précédent d'un vecteur unitaire
en posant
, on se ramène au cas précédent d'un vecteur unitaire
en posant 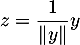 qui est unitaire et donc,
d'après la question précédente,
qui est unitaire et donc,
d'après la question précédente,
![\[\|f(z)\|=\left\|f\lp\dfrac1{\|y\|}y\rp\right\|
=\dfrac1{\|y\|}f(y)=k\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho_c/25.png)
et ainsi,
![\[\|f(y)\|=k\|y\|\]](/Generateur-Devoirs/Colles/EspaceEuclidien/isortho_c/26.png)
Tag:Espaces euclidiens
Autres sujets au hasard:

Voir aussi: