Projecteur somme de projecteurs, noyau et image
Colle de mathématiques
Sujet de colle de maths:- ProjecteursProjecteurs dans des espaces vectoriels
- Applications linéairesApplications linéaires
- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit 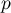 et
et 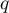 deux projecteurs d'un espace vectoriel
deux projecteurs d'un espace vectoriel 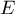 .
Montrer que
.
Montrer que
![\[\begin{array}{ll}\left( p + q \text{ projecteur}\right) &\iff \left( p\circ q=q\circ p=0\right)\\[.5em]
&\iff\Bigl(\text{Im}(p)\subset\text{Ker}(q)\text{ et }\text{Im}(q)\subset\text{Ker}(p)\Bigr)\enar\]](/Generateur-Devoirs/Colles/Applin/exP4/4.png) Dans le cas où
Dans le cas où 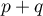 est un projecteur, montrer que
est un projecteur, montrer que 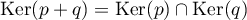 et que
et que 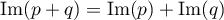 .
.
![\[\begin{array}{ll}\left( p + q \text{ projecteur}\right) &\iff \left( p\circ q=q\circ p=0\right)\\[.5em]
&\iff\Bigl(\text{Im}(p)\subset\text{Ker}(q)\text{ et }\text{Im}(q)\subset\text{Ker}(p)\Bigr)\enar\]](/Generateur-Devoirs/Colles/Applin/exP4/4.png)
Correction
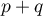 est un projecteur lorsque
est un projecteur lorsque 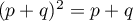 ,
or, en développant l'identité remarquable, et comme
,
or, en développant l'identité remarquable, et comme 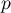 et
et 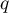 sont des projecteurs,
donc
sont des projecteurs,
donc 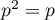 et
et 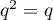 ,
,
![\[\begin{array}{ll}(p+q)^2&=(p+q)\circ(p+q)\\[.5em]
&=p^2+q^2+p\circ q+q\circ p\\[.5em]
&=p+q+p\circ q+q\circ p\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/7.png)
Ainsi, si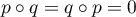 on a bien que
on a bien que 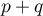 est un projecteur.
est un projecteur.
Réciproquement, si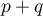 est un projecteur,
alors on doit avoir
est un projecteur,
alors on doit avoir 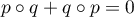 .
.
En appliquant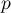 à cette relation, et comme
à cette relation, et comme 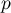 est un projecteur,
on obtient
est un projecteur,
on obtient
![\[\begin{array}{ll}
p\circ\left( p\circ q+q\circ p\right)
&=p^2\circ q+p\circ q\circ p\\[.5em]
&=p\circ q+p\circ q\circ p=0\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/14.png)
soit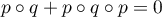 ,
,
tandis qu'en appliquant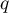 on obtient
on obtient
![\[\begin{array}{ll}
q\circ\left( p\circ q+q\circ p\right)
&=q\circ p\circ q+q^2\circ p\\[.5em]
&=q\circ p\circ q+q\circ p=0\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/17.png)
soit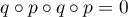 ,
,
De ces deux derniers résultats, on déduit que
![\[p\circ q\circ p=-p\circ q=-q\circ p$,
et ainsi $p\circ q=q\circ p$.
\medskip
En r\'esum\'e, si $p+q$ est un projecteur,
on a n\'ecessairement, $p\circ q+q\circ p=0 \iff p\circ q=-q\circ p$
et aussi $p\circ q=q\circ p$.
Ceci implique que $p\circ q=q\circ p=0$.
\medskip
Enfin, $p\circ q=0 \iff \lp\forall x\in E, p(q(x))=0\rp\iff \text{Im}(q)\subset{Im}(q)$
et de m\^eme en inversant les r\^oles de $p$ et $q$, d'o\`u le r\'esultat
\[\begin{array}{ll}\left( p + q \text{projecteur}\right) &\iff \left( p\circ q=q\circ p=0\right)\\[.5em]
&\iff\left( \text{Im}(p)\subset\text{Ker}(q)\text{ et }\text{Im}(q)\subset\text{Ker}(p)\rp\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/19.png)
On suppose maintenant que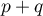 est un projecteur, ou de manière maintenant équivalente
est un projecteur, ou de manière maintenant équivalente
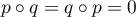 .
.
On a simplement, si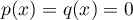 alors
alors 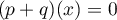 ,
c'est-à-dire
,
c'est-à-dire 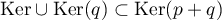 .
.
Montrons l'inclusion inverse: soit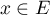 tel que
tel que 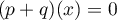 .
.
On a alors, en appliquant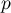 ,
,
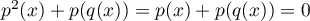 , or
, or 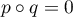 ,
ce qui implique donc
,
ce qui implique donc 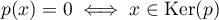 .
.
De même, en appliquant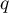 à
à 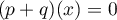 , on obtient
, on obtient
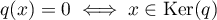 ,
et ainsi
,
et ainsi 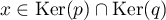 ,
d'où l'inclusion
,
d'où l'inclusion
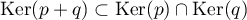 .
.
On a donc prouvé finalement que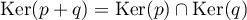 .
.
De même pour les images: on a directement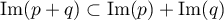 .
.
Montrons l'inclusion inverse. Soit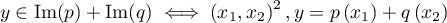
En appliquant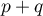 on obtient
on obtient
![\[\begin{array}{ll}
(p+q)(y)&=p^2\left( x_1\rp+q\left( p\left( x_1\rp\rp
+p\left( q\left( x_2\rp\rp+q^2\left( x_2\rp \\[.5em]
&=p\left( x_1\rp+q\left( x_2\rp\\[.5em]
&=y\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/40.png)
car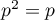 ,
, 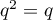 et
et 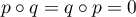 .
.
et on a donc obtenu, pour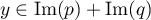 ,
,
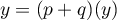 donc
donc 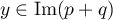 donc
donc
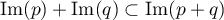 .
.
Finalement, on a donc obtenu
![\[\text{Im}(p)+\text{Im}(q)=\text{Im}(p+q)\]](/Generateur-Devoirs/Colles/Applin/exP4_c/48.png)
Correction
![\[\begin{array}{ll}(p+q)^2&=(p+q)\circ(p+q)\\[.5em]
&=p^2+q^2+p\circ q+q\circ p\\[.5em]
&=p+q+p\circ q+q\circ p\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/7.png)
Ainsi, si
Réciproquement, si
En appliquant
![\[\begin{array}{ll}
p\circ\left( p\circ q+q\circ p\right)
&=p^2\circ q+p\circ q\circ p\\[.5em]
&=p\circ q+p\circ q\circ p=0\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/14.png)
soit
tandis qu'en appliquant
![\[\begin{array}{ll}
q\circ\left( p\circ q+q\circ p\right)
&=q\circ p\circ q+q^2\circ p\\[.5em]
&=q\circ p\circ q+q\circ p=0\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/17.png)
soit
De ces deux derniers résultats, on déduit que
![\[p\circ q\circ p=-p\circ q=-q\circ p$,
et ainsi $p\circ q=q\circ p$.
\medskip
En r\'esum\'e, si $p+q$ est un projecteur,
on a n\'ecessairement, $p\circ q+q\circ p=0 \iff p\circ q=-q\circ p$
et aussi $p\circ q=q\circ p$.
Ceci implique que $p\circ q=q\circ p=0$.
\medskip
Enfin, $p\circ q=0 \iff \lp\forall x\in E, p(q(x))=0\rp\iff \text{Im}(q)\subset{Im}(q)$
et de m\^eme en inversant les r\^oles de $p$ et $q$, d'o\`u le r\'esultat
\[\begin{array}{ll}\left( p + q \text{projecteur}\right) &\iff \left( p\circ q=q\circ p=0\right)\\[.5em]
&\iff\left( \text{Im}(p)\subset\text{Ker}(q)\text{ et }\text{Im}(q)\subset\text{Ker}(p)\rp\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/19.png)
On suppose maintenant que
On a simplement, si
Montrons l'inclusion inverse: soit
On a alors, en appliquant
De même, en appliquant
On a donc prouvé finalement que
De même pour les images: on a directement
Montrons l'inclusion inverse. Soit
En appliquant
![\[\begin{array}{ll}
(p+q)(y)&=p^2\left( x_1\rp+q\left( p\left( x_1\rp\rp
+p\left( q\left( x_2\rp\rp+q^2\left( x_2\rp \\[.5em]
&=p\left( x_1\rp+q\left( x_2\rp\\[.5em]
&=y\enar\]](/Generateur-Devoirs/Colles/Applin/exP4_c/40.png)
car
et on a donc obtenu, pour
Finalement, on a donc obtenu
Tags:ProjecteursApplications linéairesEspace vectoriel
Autres sujets au hasard:

Voir aussi: