Indice de nilpotence maximal dans un espace de dimension fini
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit 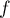 un endomorphisme non nul d'un espace de dimension fini
un endomorphisme non nul d'un espace de dimension fini 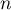 .
On suppose
.
On suppose 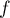 nilpotent d'indice
nilpotent d'indice 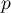 , i.e.
, i.e. 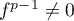 et
et 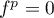 .
.
Montrer qu'il existe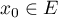 tel que la famille
tel que la famille
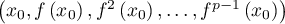 est libre.
est libre.
En déduire que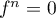 .
.
Montrer qu'il existe
En déduire que
Correction
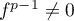 ce qui signifie justement
qu'il existe
ce qui signifie justement
qu'il existe 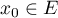 tel que
tel que 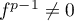 .
.
On considère alors une combinaison linéaire nulle: soit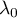 ,
, 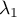 , … ,
, … , 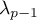 tels que
tels que
![\[\lambda_0x_0+\lambda_1f\left( x_0\rp+\lambda_2f^2\left( x_0\rp+\dots+\lambda_{p-1}f^{p-1}\left( x_0=0\]](/Generateur-Devoirs/Colles/ev/exnil_c/7.png)
Comme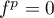 , et donc aussi
, et donc aussi 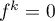 pour tout
pour tout 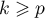 ,
en appliquant
,
en appliquant 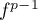 à la combinaison précédente, on obtient
à la combinaison précédente, on obtient
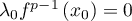 .
.
Comme on a choisit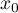 tel que
tel que 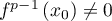 , on a donc nécessairement
, on a donc nécessairement 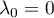 .
.
En appliquant de même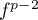 à la combinaison,
on obtient maintenant, avec
à la combinaison,
on obtient maintenant, avec 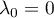 ,
,
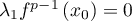 et donc, de même que précédemment,
et donc, de même que précédemment,  .
.
En réitérant, on obtient donc successivement ,
ce qui montre que la famille
,
ce qui montre que la famille
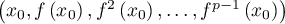 est libre.
est libre.
Il s'agit ici de montrer que l'indice de nilpotence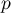 vérifie
vérifie 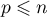 .
.
Comme cette famille est libre dans un espace de dimension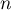 , elle contient nécessairement moins de
, elle contient nécessairement moins de 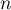 vecteurs.
Comme elle est composée de
vecteurs.
Comme elle est composée de 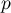 vecteurs, on a donc
vecteurs, on a donc 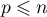 et alors, comme on l'a remarqué précédemment,
et alors, comme on l'a remarqué précédemment,
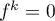 pour tout
pour tout 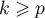 ; en particulier
; en particulier 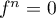 .
.
Correction
Par définition,On considère alors une combinaison linéaire nulle: soit
Comme
Comme on a choisit
En appliquant de même
En réitérant, on obtient donc successivement
Il s'agit ici de montrer que l'indice de nilpotence
Comme cette famille est libre dans un espace de dimension
Tag:Espace vectoriel
Autres sujets au hasard:

Voir aussi: