Éléments caractéristiques d'une projection orthogonale
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
- ProjecteursProjecteurs dans des espaces vectoriels
Énoncé du sujet
L'espace 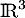 est muni de son produit scalaire usuel.
Soit
est muni de son produit scalaire usuel.
Soit 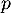 l'endomorphisme de
l'endomorphisme de 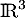 dont la matrice dans la base canonique est
dont la matrice dans la base canonique est
![\[A=\dfrac16\lp\begin{array}{ccc}2&2&-2\\2&5&1\\-2&1&5\enar\rp\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo/4.png)
![\[A=\dfrac16\lp\begin{array}{ccc}2&2&-2\\2&5&1\\-2&1&5\enar\rp\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo/4.png)
-
- Démontrer que
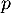 est un projection.
est un projection.
- Déterminer une base de
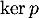 et de
et de 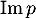 .
.
- Démontrer que
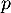 est une projection orthogonale sur un plan
est une projection orthogonale sur un plan 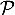 dont on donnera une équation.
dont on donnera une équation.
- Démontrer que
- Soit
 .
.
- Calculer la distance de
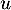 au plan
au plan 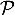 .
.
- En déduire que
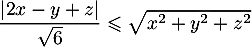 .
.
- Calculer la distance de
Correction
Correction
Oral ENSAE - Planche 10 - 2021-
- On calcule
 et on trouve que
et on trouve que  , donc que
, donc que 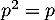 ce qui signifie exactement que
ce qui signifie exactement que  est une projection.
est une projection.
- Soit
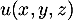 tel que
tel que 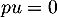 , soit aussi, en multipliant par 6,
, soit aussi, en multipliant par 6,
![\[6Au=0\iff\la\begin{array}{rcrcrcl}2x&+&2y&-&2z&=&0\\2x&+&5y&+&z&=&0\\-2x&+&y&+&5z&=&0\enar\right.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/7.png)
d'où, avec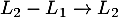 et
et  ,
,
![\[\la\begin{array}{rcrcrcl}2x&+&2y&-&2z&=&0\\&&3y&+&3z&=&0\\&&3y&+&3z&=&0\enar\right.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/10.png)
On trouve donc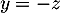 et
et  , et donc
, et donc
![\[\ker p=\text{Vect}\Bigl\{ u_0(2,-1,1)\Bigr\}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/13.png)
Maintenant on sait, d'après le théorème du rang, que l'image de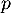 est de dimension 2. Il suffit donc de prendre l'image de deux vecteurs, les images des deux premiers vecteurs de la base canonique donc les deux premières colonnes de la matrice et de vérifier que ces deux vecteurs images ne sont pas liés.
est de dimension 2. Il suffit donc de prendre l'image de deux vecteurs, les images des deux premiers vecteurs de la base canonique donc les deux premières colonnes de la matrice et de vérifier que ces deux vecteurs images ne sont pas liés.
On pose donc
![\[u_1=6p(e_1)=(2,2,-2)\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/15.png)
et
![\[u_2=6p(e_2)=(2,5,1)\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/16.png)
Ces deux vecteurs ne sont pas colinéaires et forment donc une base de l'image de qui est donc
qui est donc
![\[\text{Im} p = \text{Vect}\Bigl\{ u_1, u_2\Bigr\}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/18.png)
-
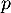 est maintenant de plus une projection orthogonale si son image et son noyau sont orthogonales, ici avec la produits scalaires
est maintenant de plus une projection orthogonale si son image et son noyau sont orthogonales, ici avec la produits scalaires
![\[\langle u_0, u_1\rangle = 4-2-2=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/20.png)
et
![\[\langle u_0, u_2\rangle = 4-5+1=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/21.png)
ce qui montre bien que l'image et le noyau de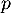 sont orthogonaux et donc que
sont orthogonaux et donc que 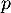 est une projection orthogonale.
est une projection orthogonale.
Le plan est l'image de
est l'image de 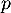 .
Soit maintenant
.
Soit maintenant 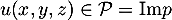 , alors on a
, alors on a
![\[\langle u, u_0\rangle=0\iff 2x-y+z=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/27.png)
qui est l'équation du plan image recherchée.
- On calcule
-
- La distance de
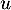 au plan
au plan  est
est 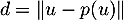 , qu'il reste à calculer.
, qu'il reste à calculer.
![\[\begin{array}{ll}
u-Au&=\dfrac16\lp\begin{array}{ccc}4x-2y+2z\\-2x+y-z\\2x-y+z\enar\rp\\[1.8em]
&=\dfrac16\lp\begin{array}{ccc}2(2x-y+z)\\-(2x-y+z)\\2x-y+z\enar\right)
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/31.png)
d'où la distance
![\[\begin{array}{ll}d&=\|u-p(u)\|^2\\
&=\dfrac1{6^2}\Bigl(\lp2^2+(-1)^2+1^2\rp\lp2x-y+z\rp^2\Bigr)\\
&=\dfrac1{\sqrt6}\lp2x-y+z\right)
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/32.png)
- La distance minimise la norme, et on a donc (d'après Pythagore aussi)
![\[\forall u\in\R^3, \, \|u-p(u)\|\leqslant\|u\|\]](/Generateur-Devoirs/Colles/EspaceEuclidien/expo_c/33.png)
qui est directement exactement l'ingélité recherchée.
- La distance de
Tags:Espaces euclidiensProjecteurs
Autres sujets au hasard:

Voir aussi: