Produit scalaire avec des polynômes, base orthonormale et calcul de distance
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
- PolynômePolynômes
Énoncé du sujet
Soient ![$E=\R_n[X]$](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3/1.png) et
et  des réels distincts.
On pose, pour
des réels distincts.
On pose, pour 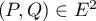 ,
,
![\[\langle P,Q\rangle=\sum_{k=0}^n P(a_k)Q(a_k).\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3/4.png)
![\[\langle P,Q\rangle=\sum_{k=0}^n P(a_k)Q(a_k).\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3/4.png)
- Vérifier qu'on définit un produit scalaire sur
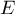 .
.
- Déterminer une base orthonormée de
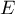 .
.
- Déterminer la distance de
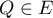 au sous-espace
au sous-espace
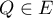
Correction
Correction
- Il est clair qu'on définit ainsi une forme bilinéaire symétrique et que
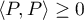 . De plus, si
. De plus, si
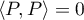 , alors
, alors
![\[\sum_{k=0}^n P^2(a_k)=0\implies P(a_k)=0 \text{ pour } k=1,\dots,n\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/3.png)
Or, un polynôme de degré au plus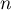 ayant au moins
ayant au moins 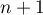 racines est nécessairement le polynôme nul.
racines est nécessairement le polynôme nul.
Donc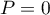 et la forme bilinéaire est définie positive : c'est un produit scalaire.
et la forme bilinéaire est définie positive : c'est un produit scalaire.
- Contrairement à ce que l'on fait souvent, ici, utiliser le procédé de Gram-Schmidt pour trouver une base
orthonormale n'est pas la meilleure idée.
On peut plutôt raisonner en terme de racines et voir que si
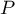 s'annule en
beaucoup de
s'annule en
beaucoup de 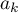 , alors
, alors 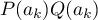 sera souvent nul. On va donc définir, pour
sera souvent nul. On va donc définir, pour 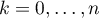
![\[P_k=\prod_{j\neq k}(X-a_j)\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/11.png)
Pour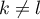 , on a
, on a
![\[\langle P_k,P_l\rangle=P_k(a_k)P_l(a_k)=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/13.png)
La famille est donc orthogonale. On l'orthonormalise finalement en remarquant que
![\[\|P_k\|^2=\prod_{j\neq k}(a_k-a_j)^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/14.png)
et on pose donc
![\[Q_k=\frac{P_k}{\dsp\prod_{j\neq k}(a_k-a_j)}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/15.png)
 est une famille orthonormale de
est une famille orthonormale de 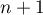 éléments dans un espace de dimension
éléments dans un espace de dimension 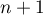 .
C'est une base de
.
C'est une base de ![$\R_n[X]$](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/19.png) .
.
- On va trouver un vecteur normal à l'hyperplan
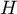 . C'est très facile en regardant la définition de
. C'est très facile en regardant la définition de 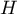 , car
si on pose
, car
si on pose 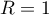 , on a
, on a
![\[\langle P,R\rangle=\sum_{k=0}^n P(a_k)\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/23.png)
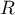 est donc un vecteur normal à
est donc un vecteur normal à 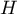 .
.
Par une formule du cours (très facile à retrouver par un dessin), on en déduit que la distance de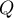 à
à 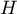 est
est
![\[\frac{\langle Q,R\rangle}{\|R\|}=\dfrac{\dsp\sum_{k=0}^n Q(a_k)}{\sqrt{n+1}}.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex3_c/28.png)
Tags:Espaces euclidiensPolynôme
Autres sujets au hasard:

Voir aussi: