Matrice d'une projection orthogonale - Distance à un sous-espace
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
- ProjecteursProjecteurs dans des espaces vectoriels
- MatricesMatrices
Énoncé du sujet
Soit  muni de son produit scalaire canonique et de la base canonique
muni de son produit scalaire canonique et de la base canonique  .
.
On considère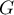 le sous-espace vectoriel défini par les équations
le sous-espace vectoriel défini par les équations
![\[\la\begin{array}{rcl}
x_1+x_2&=&0\\
x_3+x_4&=&0.
\enar\right.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex4/4.png)
On considère
- Déterminer une base orthonormale de
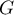 .
.
- Déterminer la matrice dans
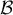 de la projection orthogonale
de la projection orthogonale  sur
sur  .
.
- Soit
 un élément de
un élément de 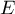 .
Déterminer la distance de
.
Déterminer la distance de  à
à  .
.
Correction
Correction
- On commence par trouver une base de
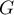 . Mais on a
. Mais on a
![\[\la\begin{array}{rcl}
x_1+x_2&=&0\\
x_3+x_4&=&0\\
\enar\right.
\iff\la\begin{array}{rcl}
x_1&=&x_1\\
x_2&=&-x_1\\
x_3&=&x_3\\
x_4&=&-x_3.
\enar\right.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex4_c/2.png)
On en déduit que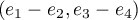 est une base de
est une base de 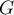 .
Ces deux vecteurs sont déjà orthogonaux, il suffit de les normaliser.
Si on pose
.
Ces deux vecteurs sont déjà orthogonaux, il suffit de les normaliser.
Si on pose 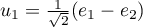 ,
, 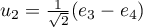 , alors
, alors  est une base orthonormale de
est une base orthonormale de 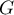 .
.
- On calcule
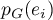 par
par
![\[p_G(e_i)=\langle e_i,u_1\rangle u_1+\langle e_i,u_2\rangle u_2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex4_c/10.png)
On en déduit que la matrice de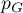 dans la base canonique est
dans la base canonique est
![\[\frac 12\lp\begin{array}{cccc}
1&-1&0&0\\
-1&1&0&0\\
0&0&1&-1\\
0&0&-1&1
\enar\rp\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex4_c/12.png)
- On sait que
 .
.
Avec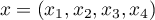 , on a
, on a
![\[p_G(x)=\dfrac 12(x_1-x_2,-x_1+x_2,x_3-x_4,-x_3+x_4)\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex4_c/15.png)
et donc
![\[x-p_G(x)=\dfrac 12(x_1+x_2,x_1+x_2,x_3+x_4,x_3+x_4).\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex4_c/16.png)
Il vient
![\[d(x,G)^2=\dfrac 12\lp(x_1+x_2)^2+(x_3+x_4)^2\rp.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex4_c/17.png)
Tags:Espaces euclidiensProjecteursMatrices
Autres sujets au hasard:

Voir aussi: