Matrice avec un paramètre: diagonalisable ?
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
- MatricesMatrices
Énoncé du sujet
Soit 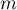 un nombre réel et
un nombre réel et 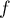 l'endomorphisme de
l'endomorphisme de 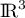 dont la matrice dans la base canonique est
dont la matrice dans la base canonique est
![\[A=\lp\begin{array}{rcl}
1&0&1\\
-1&2&1\\
2-m&m-2&m
\end{array}\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03/4.png)
Déterminer les valeurs propres de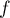 ,
et préciser pour quelles valeurs de
,
et préciser pour quelles valeurs de 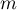 l'endomorphisme est diagonalisable.
l'endomorphisme est diagonalisable.
![\[A=\lp\begin{array}{rcl}
1&0&1\\
-1&2&1\\
2-m&m-2&m
\end{array}\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03/4.png)
Déterminer les valeurs propres de
Correction
On calcule le polynôme caractéristique de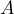 . On a
. On a
![\[\chi_A(X)=\left|\begin{array}{ccc}
1-X&0&1\\
-1&2-X&1\\
2-m&m-2&m-X
\enar\right|\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/2.png)
soit, avec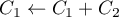 ,
,
![\[\chi_A(X)=\left|
\begin{array}{ccc}
1-X&0&1\\
1-X&2-X&1\\
0&m-2&m-X
\enar\right|\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/4.png)
puis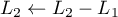
![\[\begin{array}{ll}\chi_A(X)&=\left|\begin{array}{ccc}
1-X&0&1\\
0&2-X&0\\
0&m-2&m-X
\enar\right|\\[2em]
&=(1-X)\left|\begin{array}{cc}
2-X&0\\
m-2&m-X
\end{array}\right|\\[1.5em]
&=(1-X)(2-X)(m-X)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/6.png)
Les valeurs propres de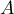 sont donc 1,2 et
sont donc 1,2 et 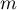 .
En particluier, si
.
En particluier, si 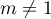 et
et 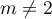 ,
, 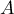 admet trois valeurs
propres distinctes et est donc diagonalisable.
admet trois valeurs
propres distinctes et est donc diagonalisable.
Par contre, si ou
ou  ,
, 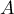 n'admet que deux valeurs propres.
n'admet que deux valeurs propres.
Si , la valeur propre
, la valeur propre 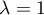 est double et il faut connaître
la dimensions de de l'espace propre associé.
est double et il faut connaître
la dimensions de de l'espace propre associé.
Pour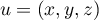 , on a
, on a
![\[f(u)=u\iff
\la\begin{array}{rcl}
z&=&0\\
-x+y+z&=&0\\
x-y&=&0\\
\enar\right.
\iff
\left\{}\newcommand{\ra}{\right\}
\begin{array}{rcl}
x&=&x\\
y&=&x\\
z&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/18.png)
Une base de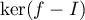 est donc donnée par le vecteur
est donc donnée par le vecteur 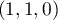 et cet espace propre est de dimension
et cet espace propre est de dimension 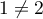 : la matrice, et l'endomorphisme,
n'est pas diagonalisable.
: la matrice, et l'endomorphisme,
n'est pas diagonalisable.
Si , c'est la valeur propre
, c'est la valeur propre 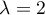 qui est cette fois double,
et l'espace propre associé est donné par
qui est cette fois double,
et l'espace propre associé est donné par
![\[f(u)=2u\iff
\la\begin{array}{rcl}
-x+z&=&0\\
-x+z&=&0\\
0&=&0\\
\enar\right.
\iff
\la\begin{array}{rcl}
x&=&x\\
y&=&y\\
z&=&x
\enar\right.\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/24.png)
On a alors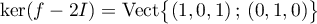 , et
en particulier,
, et
en particulier, 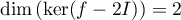 et
et 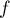 est cette fois
diagonalisable.
est cette fois
diagonalisable.
Méthode 2: avec un calcul de rang
On calcule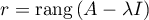 :
:
![\[r=\text{rg}
\lp\begin{array}{ccc}1-\lambda&0&1\\-1&2-\lambda&1\\2-m&m-2&m-\lambda\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/29.png)
soit, intervertissant les lignes 1 et 2: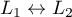
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\1-\lambda&0&1\\2-m&m-2&m-\lambda\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/31.png)
puis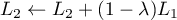 et
et 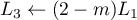 :
:
![\[\begin{array}{ll}r&=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\0&(1-\lambda)(2-\lambda)&2-\lambda\\
0&m-2+(2-m)(2-\lambda)&2-\lambda\enar\rp\\[2.2em]
&=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\0&(1-\lambda)(2-\lambda)&2-\lambda\\
0&(2-m)(1-\lambda)&2-\lambda\enar\right)
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/34.png)
puis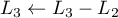 :
:
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\0&(1-\lambda)(2-\lambda)&2-\lambda\\
0&(1-\lambda)(\lambda-m)&0\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/36.png)
et enfin, simplement pour finir le pivot de Gauss et obtenir une matrice triangulaire, on intervertit les deux dernières colonnes: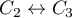
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&1&2-\lambda\\0&2-\lambda&(1-\lambda)(2-\lambda)\\
0&0&(1-\lambda)(\lambda-m)\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/38.png)
On a maintenant un rang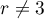 pour
pour
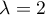 , ou
, ou 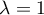 ou encore
ou encore  .
.
Ainsi, si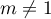 et
et 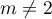 , la matrice a trois valeurs propres
distinctes et est donc diagonalisables.
, la matrice a trois valeurs propres
distinctes et est donc diagonalisables.
Il reste à étudier les cas et
et  .
.
Supposons alors
alors 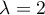 est valeur propre simple,
et
est valeur propre simple,
et 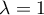 est valeur propre double avec
est valeur propre double avec
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&1&1\\0&1&0\\
0&0&0\enar\rp=2\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/50.png)
La dimension de l'espace propre associé est donc 1 et la matrice n'est pas diagonalisable.
Supposons alors
alors 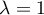 est valeur propre simple,
et
est valeur propre simple,
et 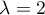 est valeur propre double avec
est valeur propre double avec
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&1&0\\0&0&0\\
0&0&0\enar\rp=1\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/54.png)
La dimension de l'espace propre associé est cette fois 2 et la matrice est diagonalisable.
Correction
Méthode 1: avec le polynôme caractéristiqueOn calcule le polynôme caractéristique de
![\[\chi_A(X)=\left|\begin{array}{ccc}
1-X&0&1\\
-1&2-X&1\\
2-m&m-2&m-X
\enar\right|\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/2.png)
soit, avec
![\[\chi_A(X)=\left|
\begin{array}{ccc}
1-X&0&1\\
1-X&2-X&1\\
0&m-2&m-X
\enar\right|\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/4.png)
puis
![\[\begin{array}{ll}\chi_A(X)&=\left|\begin{array}{ccc}
1-X&0&1\\
0&2-X&0\\
0&m-2&m-X
\enar\right|\\[2em]
&=(1-X)\left|\begin{array}{cc}
2-X&0\\
m-2&m-X
\end{array}\right|\\[1.5em]
&=(1-X)(2-X)(m-X)\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/6.png)
Les valeurs propres de
Par contre, si
Si
Pour
Une base de
Si
![\[f(u)=2u\iff
\la\begin{array}{rcl}
-x+z&=&0\\
-x+z&=&0\\
0&=&0\\
\enar\right.
\iff
\la\begin{array}{rcl}
x&=&x\\
y&=&y\\
z&=&x
\enar\right.\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/24.png)
On a alors
Méthode 2: avec un calcul de rang
On calcule
![\[r=\text{rg}
\lp\begin{array}{ccc}1-\lambda&0&1\\-1&2-\lambda&1\\2-m&m-2&m-\lambda\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/29.png)
soit, intervertissant les lignes 1 et 2:
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\1-\lambda&0&1\\2-m&m-2&m-\lambda\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/31.png)
puis
![\[\begin{array}{ll}r&=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\0&(1-\lambda)(2-\lambda)&2-\lambda\\
0&m-2+(2-m)(2-\lambda)&2-\lambda\enar\rp\\[2.2em]
&=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\0&(1-\lambda)(2-\lambda)&2-\lambda\\
0&(2-m)(1-\lambda)&2-\lambda\enar\right)
\enar\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/34.png)
puis
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&2-\lambda&1\\0&(1-\lambda)(2-\lambda)&2-\lambda\\
0&(1-\lambda)(\lambda-m)&0\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/36.png)
et enfin, simplement pour finir le pivot de Gauss et obtenir une matrice triangulaire, on intervertit les deux dernières colonnes:
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&1&2-\lambda\\0&2-\lambda&(1-\lambda)(2-\lambda)\\
0&0&(1-\lambda)(\lambda-m)\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/38.png)
On a maintenant un rang
Ainsi, si
Il reste à étudier les cas
Supposons
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&1&1\\0&1&0\\
0&0&0\enar\rp=2\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/50.png)
La dimension de l'espace propre associé est donc 1 et la matrice n'est pas diagonalisable.
Supposons
![\[r=\text{rg}
\lp\begin{array}{ccc}-1&1&0\\0&0&0\\
0&0&0\enar\rp=1\]](/Generateur-Devoirs/Colles/Diagonalisation/ex03_c/54.png)
La dimension de l'espace propre associé est cette fois 2 et la matrice est diagonalisable.
Tags:DiagonalisationMatrices
Autres sujets au hasard:

Voir aussi: