Puissance n-ième d'une matrice 2x2 symétrique
Colle de mathématiques
Sujet de colle de maths:- DiagonalisationDiagonalisation de matrice et réduction des endomorphismes
- MatricesMatrices
Énoncé du sujet
Soit 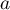 et
et  deux réels et
deux réels et 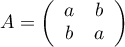 .
Calculer
.
Calculer 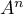 pour tout entier
pour tout entier 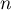 .
.
Correction
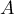 .
Son polynôme caractéristique est
.
Son polynôme caractéristique est
![\[\chi_A(X)=\det\left( A-XI_3\right)
=\left|\begin{array}{cc}a-X&b\\b&a-X\enar\right|
=(a-X)^2-b^2=(a-X+b)(a-X-b)\]](/Generateur-Devoirs/Colles/Diagonalisation/ex2_c/2.png)
Ainsi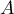 est diagonalisable avec comme valeurs propres
est diagonalisable avec comme valeurs propres
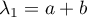 et
et 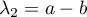 .
.
L'espace propre associé à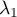 est engendré
par
est engendré
par 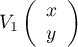 avec
avec 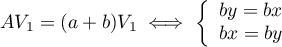 Si
Si 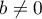 , sinon
, sinon 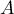 est déjà diagonale et
est déjà diagonale et
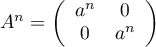 ,
on trouve donc
,
on trouve donc  et
et 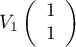 .
.
De même, l'espace propre associé à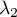 est engendré par
est engendré par 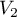 avec
avec 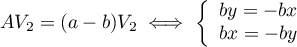 et on trouve, toujours pour
et on trouve, toujours pour  ,
, 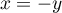 et
et  .
.
La matrice de passage de la base canonique à la base de vecteurs propres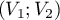 est
est
 , et on a la relation
, et on a la relation
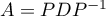 , puis
, puis
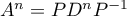 ,
,
avec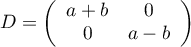 ,
donc
,
donc 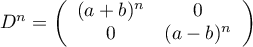 ,
,
et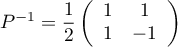
d'où
![\[A^n=PD^nP^{-1}
=\dfrac12\lp\begin{array}{cc}(a+b)^n+(a-b)^n&(a+b)^n-(a-b)^n\\
(a+b)^n-(a-b)^n&(a+b)^n+(a-b)^n\enar\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ex2_c/27.png)
Correction
On cherche à diagonaliserAinsi
L'espace propre associé à
De même, l'espace propre associé à
La matrice de passage de la base canonique à la base de vecteurs propres
avec
et
d'où
Tags:DiagonalisationMatrices
Autres sujets au hasard:

Voir aussi: