Loi d'un produit
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
Soit  une variable aléatoire qui suit une loi normale centrée réduite.
Soit
une variable aléatoire qui suit une loi normale centrée réduite.
Soit 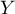 une variable aléatoire, indépendante de
une variable aléatoire, indépendante de 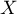 ,
et telle que
,
et telle que 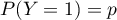 et
et 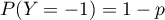 .
.
Montrer que a la même loi que
a la même loi que  .
.
Montrer que
Correction
 , soit
, soit
![\[F_Z(x)=P(Z\leq x)=P(XY\leq x)\]](/Generateur-Devoirs/Colles/VAC/prprod_c/2.png) Comme
Comme 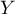 ne peut prendre que deux valeurs,
on peut utiliser la formule des probabilités totales:
ne peut prendre que deux valeurs,
on peut utiliser la formule des probabilités totales:
![\[\begin{array}{ll}
F_Z(x)&=P(XY\leq x)\\[.5em]
&=P\bigl((XY\leq x)\cap(Y=1)\bigr)
+P\bigl((XY\leq x)\cap(Y=-1)\bigr)\\[.5em]
&=P\bigl((Y\leq x)\cap(Y=1)\bigr)
+P\bigl((-Y\leq x)\cap(Y=-1)\bigr)
\enar\]](/Generateur-Devoirs/Colles/VAC/prprod_c/4.png) et, par indépendance des variables
et, par indépendance des variables
![\[F_Z(x)=p\,P(Y\leq x)+(1-p)\,P(-Y\leq x)\]](/Generateur-Devoirs/Colles/VAC/prprod_c/5.png)
et donc, avec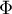 la fonction de répartion de la loi normale centrée réduite
la fonction de répartion de la loi normale centrée réduite
![\[\begin{array}{ll}
F_Z(x)
&=p\,\Phi(x)+(1-p)\,P(Y\geq -x)\\[.5em]
&=p\,\Phi(x)+(1-p)\,(1-\Phi(-x))\\[.5em]
&=p\,\Phi(x)+(1-p)\,\Phi(x)\\[.5em]
&=\Phi(x)
\enar\]](/Generateur-Devoirs/Colles/VAC/prprod_c/7.png)
Ainsi, et donc
et donc 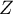 suit aussi la loi normale centrée réduite.
suit aussi la loi normale centrée réduite.
Correction
On cherche la fonction de répartition de la variable![\[\begin{array}{ll}
F_Z(x)&=P(XY\leq x)\\[.5em]
&=P\bigl((XY\leq x)\cap(Y=1)\bigr)
+P\bigl((XY\leq x)\cap(Y=-1)\bigr)\\[.5em]
&=P\bigl((Y\leq x)\cap(Y=1)\bigr)
+P\bigl((-Y\leq x)\cap(Y=-1)\bigr)
\enar\]](/Generateur-Devoirs/Colles/VAC/prprod_c/4.png)
et donc, avec
![\[\begin{array}{ll}
F_Z(x)
&=p\,\Phi(x)+(1-p)\,P(Y\geq -x)\\[.5em]
&=p\,\Phi(x)+(1-p)\,(1-\Phi(-x))\\[.5em]
&=p\,\Phi(x)+(1-p)\,\Phi(x)\\[.5em]
&=\Phi(x)
\enar\]](/Generateur-Devoirs/Colles/VAC/prprod_c/7.png)
Ainsi,
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: