Racine carrée d'une différence d'exponentielles
Colle de mathématiques
Sujet de colle de maths:- Variables aléatoires continuesVariables aléatoires continues
Énoncé du sujet
oral HEC, BL - 2022 - Exercice sans préparation.
Soit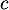 un réel strictement positif. On note
un réel strictement positif. On note 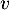 l'application définie sur
l'application définie sur  par:
par:
![\[v(x)=\la\begin{array}{lll}0&\text{si}&x\leqslant0\\
\dfrac{e^{-c^2x}-e^{-4c^2x}}{x\ln4}&\text{si}&x>0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2/4.png)
On admet que est une fonction densité de probabilité, et on note
est une fonction densité de probabilité, et on note 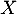 une variable aléatoire de densité
une variable aléatoire de densité 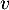 .
.
Soit
![\[v(x)=\la\begin{array}{lll}0&\text{si}&x\leqslant0\\
\dfrac{e^{-c^2x}-e^{-4c^2x}}{x\ln4}&\text{si}&x>0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2/4.png)
On admet que
- Montrer que
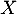 admet une espérance et calculer sa valeur.
admet une espérance et calculer sa valeur.
- On note
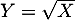 . On admet que
. On admet que 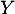 est une variable à densité.
est une variable à densité.
Montrer que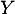 admet une espérance et une variance et donner leurs valeurs.
admet une espérance et une variance et donner leurs valeurs.
Correction
Correction
oral HEC, BL - 2022 - Exercice sans préparation.-
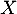 admet une espérance si et seulement si
admet une espérance si et seulement si
![\[\begin{array}{ll}E(X)&=\dsp\int_{-\infty}^{+\infty}xv(x)\,dx\\
&=\dfrac1{\ln4}\dsp\int_0^{+\infty} \left( e^{-c^2x}-e^{-4c^2x}\rp\,dx\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/2.png)
converge, ce qui est le cas, et on sait même facilement calculer cette intégrale
![\[\begin{array}{ll}E(X)&=\dfrac1{\ln4}\lb\dfrac{-1}{c^2}e^{-c^2x}\rb_0^{+\infty} -
\dfrac1{\ln4}\lb\dfrac{-1}{4c^2}e^{-4c^2x}\rb_0^{+\infty}\\
&=\dfrac1{\ln4}\left( \dfrac1{c^2}-\dfrac1{4c^2}\rp\\
&=\dfrac3{4c^2\ln4}\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/3.png)
- On
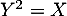 et
et 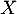 admet une espérance, donc
admet une espérance, donc 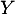 admet un moment d'ordre 2, donc une espérance et un variance.
admet un moment d'ordre 2, donc une espérance et un variance.
Pour revenir à la loi de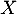 , on passe classiquement par la fonction de répartition:
, on passe classiquement par la fonction de répartition:
![\[\begin{array}{ll}F_Y(x)&=P(Y\leqslant x)\\
&=P(\sqrt{X}\leqslant x)\\
&=P(X\leqslant x^2)\\
&=F_X(x^2)\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/8.png)
et on revient à la densité en dérivant cette fonction de répartition:
![\[F_Y'(x)=2xF_X'(x^2)=2xv(x^2)\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/9.png)
et on a alors l'espérance
![\[E(Y) = \dfrac2{\ln4}\int_0^{+\infty}\left( e^{-c^2x^2}-e^{-4c^2x^2}\rp\,dx\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/10.png)
Il reste à calculer ces intégrales: on pose
![\[I_1=\int_0^{+\infty} e^{-c^2x^2}dx\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/11.png)
et
![\[I_2=\int_0^{+\infty} e^{-4c^2x^2}dx\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/12.png)
en utilisant l'intégrale de la densité de la loi normale.
On sait en effet, grâce à la loi normale centrée réduite, que
![\[\int_{-\infty}^{+\infty}\dfrac1{\sqrt{2\pi}}e^{-x^2/2}dx=1\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/13.png)
d'où, par symétrie,
![\[I=\int_0^{+\infty}e^{-x^2/2}dx=\dfrac{\sqrt{2\pi}}2\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/14.png)
Avec le changement de variable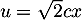 , on obtient
, on obtient
![\[\begin{array}{ll}I_1&=\dsp\int_0^{+\infty} e^{-u^2/2}\dfrac1{\sqrt2 c} du\\
&=\dfrac1{\sqrt2 c}I =\dfrac{\sqrt\pi}{2c}
\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/16.png)
De même, en posant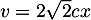 on obtient
on obtient
![\[\begin{array}{ll}I_2&=\dsp\int_0^{+\infty} e^{-v^2/2}\dfrac1{2\sqrt2c}dv\\
&=\dfrac1{2\sqrt2c}I=\dfrac{\sqrt\pi}{4c}
\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/18.png)
Finalement, on trouve donc par linéarité de l'intégrale
![\[E(Y)=\dfrac2{\ln4}\left( I_1-I_2\right)
=\dfrac{\sqrt\pi}{4c\ln2}\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/19.png)
On peut enfin calculer la vairance à l'aide de la formule de König-Huygens:
![\[\begin{array}{ll}V(Y)&=E(Y^2)-E(Y)^2\\
&=E(X)-E(Y)^2\\
&=\dfrac3{4c^2\ln4}-\lp\dfrac{\sqrt\pi}{4c\ln2}\rp^2\\
&=\dfrac{6\ln2-\pi}{16c^2\ln^22}
\enar\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-1.2_c/20.png)
Tag:Variables aléatoires continues
Autres sujets au hasard:

Voir aussi: