Limite nulle et comparaison suite géométrique
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
- Donner la définition de
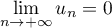 .
.
- Soit
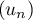 une suite qui vérifie, pour tout entier
une suite qui vérifie, pour tout entier 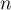 ,
,
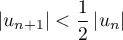 .
Montrer que
.
Montrer que 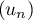 tend vers 0.
tend vers 0.
- Soit
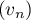 une suite de réels non nuls vérifiant
une suite de réels non nuls vérifiant
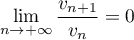 .
Prouver que
.
Prouver que 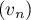 converge vers 0.
converge vers 0.
Correction
Correction
- cf. cours...
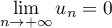
siginifie que
![\[\forall\varepsilon>0,\exists N\in\N,\forall n\geqslant N, \left|u_n\right|<\varepsilon\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/2.png)
- On a rapidement par récurrence que, pour tout entier
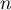 ,
,
En effet, on a![\[\left|u_n\right|<\lp\dfrac12\rp^n\left|u_0\right|\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/4.png)
 , puis si
on suppose, pour un certain entier
, puis si
on suppose, pour un certain entier 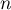 , que
, que
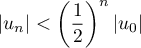 ,
alors au rang suivant,
,
alors au rang suivant,
![\[\left|u_{n+1}\right|<\dfrac12\left|u_n\right|\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/8.png)
et donc, par hypothèse de récurrence,
![\[\left|u_{n+1}\right|<\dfrac12\,\lp\dfrac12\rp^n\left|u_0\right|\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/9.png)
ce qui montre que la propriété est héréditaire, et donc vraie pour tout entier d'après le principe de récurrence.
d'après le principe de récurrence.
Maintenant, comme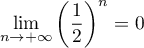 , on en déduit que
, on en déduit que
![\[\lim_{n\to+\infty}u_n=0\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/12.png)
- Par définition de la limite nulle, on a donc
![\[\forall\varepsilon>0,\exists N\in\N,\forall n\geqslant N, \left|\dfrac{v_{n+1}}{v_n}\right|<\varepsilon\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/13.png)
Ceci étant vrai pour tout , on peut choisir
, on peut choisir  , afin de pouvoir utiliser le résultat de la question précédente.
, afin de pouvoir utiliser le résultat de la question précédente.
Il existe alors un entier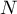 tel que, pour tout entier
tel que, pour tout entier 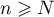 , on a
, on a
![\[\left|\dfrac{v_{n+1}}{v_n}\right|<\dfrac12
\iff\left|v_{n+1}\right|<\dfrac12\left|v_n\right|\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/18.png)
Comme dans la question précédente, on prouve alors (par récurrence) que, pour tout entier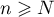 ,
,
![\[\left|v_n\right|<\lp\dfrac12\rp^{n-N}\left|v_N\right|\]](/Generateur-Devoirs/Colles/Suites/ex2.5_c/20.png)
et, à nouveau comme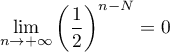 , on en déduit
que
, on en déduit
que  tend vers 0.
tend vers 0.
Tags:SuitesLimite
Autres sujets au hasard:

Voir aussi: