Détermination d'une limite
Colle de mathématiques
Sujet de colle de maths:- LimiteLimites de suites et de fonctions
Énoncé du sujet
Déterminer la limite
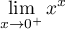
Correction
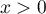 ,
,
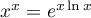 .
.
Or,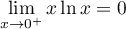 , par croissances comparées.
, par croissances comparées.
On trouve donc, que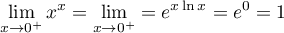 .
.
Correction
On a, pourOr,
On trouve donc, que
Tag:Limite
Autres sujets au hasard:

Voir aussi: