Inégalité des accroissements finis - Convergence d'une suite


Colle de mathématiques

Sujet de colle de maths:
  • SuitesSuites
  • Rolle - AFThéorème de Rolle et théorème des accroissements finis

Énoncé du sujet

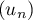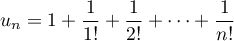On considère la suite $\left( u_n\rp$ définie par $u_n=1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dots+\dfrac{1}{n!}$.
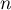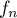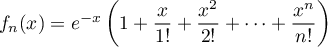Pour tout entier $n$, on définit de plus la fonction $f_n$ définie par $f_n(x)=e^{-x}\lp1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dots+\dfrac{x^n}{n!}\rp$.

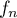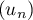En utilisant l'inégalité des accroissements finis appliquée à $f_n$ sur $[0;1]$ montrer la suite $\left( u_n\rp$ converge, et déterminer sa limite.


Correction

Correction

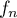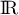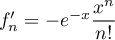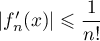$f_n$ est dérivable sur $\R$ avec $f_n'=-e^{-x}\dfrac{x^n}{n!}$ et donc, pour $x\in[0;1]$, on a $\left|f_n'(x)\right|\leqslant\dfrac{1}{n!}$.
Ainsi, d'après l'inégalité des accroissement finis sur $[0;1]$, on obtient donc
\[ \left|f_n(1)-f_n(0)\right|\leqslant\dfrac{1}{n!} \]

soit
\[ \left|\frac{u_n}{e}-1\right|\leqslant\dfrac{1}{n!} \]

ce qui montre que $\dsp\lim_{n\to+\infty}u_n=e$.


Tags:SuitesRolle - AF

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0