Familles libres et génératrices
Colle de mathématiques
Sujet de colle de maths:- Espace vectorielEspaces vectoriels
Énoncé du sujet
Parmi les familles suivantes de vecteurs de 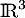 , déterminer lesquelles sont libres, et lesquelles sont génératrices.
, déterminer lesquelles sont libres, et lesquelles sont génératrices.
-
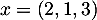 ;
; 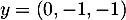 et
et 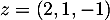
-
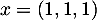 et
et 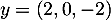
-
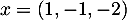 ;
; 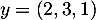 et
et 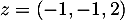
-
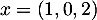 ;
; 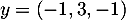 ;
; 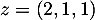 et
et 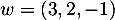
Correction
Correction
- Une combinaison linéaire nulle des ces trois premiers vecteurs:
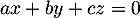 est le système
est le système
![\[\la\begin{array}{rcrcrcc}
2a&& &+&2b &=&0\\
a&-&b&-&c&=&0\\
3a&+&b&-&c&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/ev/exlibre_c/2.png)
La première équation donne directement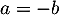 et qui donne dans les deux autres équations
et qui donne dans les deux autres équations
![\[\la\begin{array}{rcrcr}
-2b&-&c&=&0\\
-2b&-&c&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/ev/exlibre_c/4.png)
Ce système n'est donc pas un système de Cramer, et d'autres solutions que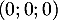 existent. En particulier la famille
existent. En particulier la famille 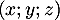 n'est pas libre.
n'est pas libre.
On a donc aussi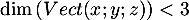 et cette famille ne peut donc pas être génératrice de
et cette famille ne peut donc pas être génératrice de 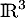 puisque
puisque 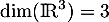 .
.
- Cette famille de 2 vecteurs ne peut pas être génératrice d'un espace de dimension 3. La famille est par contre libre, puisque ces deux vecteurs ne sont pas colinéaires (les coordonnées ne sont pas proportionelles).
- Une combinaison linéaire nulle des ces trois premiers vecteurs:
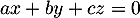 est le système
est le système
![\[\la\begin{array}{rcrcrcc}
a&+&2b&-&c &=&0\\
-a&+&3b&-&c&=&0\\
-2a&+&b&+&2c&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/ev/exlibre_c/11.png)
En soustrayant les deux premières équations,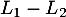 , on obtient l'équation
, on obtient l'équation 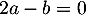 , et en ajoutant les trois équations,
, et en ajoutant les trois équations, 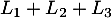 , on obtient
, on obtient 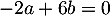 , soit le système
, soit le système
![\[\la\begin{array}{rcrcr}
2a&-&b&=&0\\
-2a&+&6b&=&0
\enar\right.\]](/Generateur-Devoirs/Colles/ev/exlibre_c/16.png)
Il s'agit d'un système de Cramer (de déterminant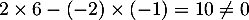 ) et qui admet donc une unique solution
) et qui admet donc une unique solution 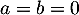 . On trouve alors aussi que
. On trouve alors aussi que 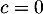 , ce qui finit de montrer que la famille
, ce qui finit de montrer que la famille 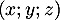 est libre.
est libre.
C'est donc une famille libre de trois vecteurs dans un espace de dimension 3: c'est donc une base qui est aussi en particulier génératrice.
- Cette dernière famille ne paut pas être libre car elle possède trop d'éléments, plus de
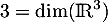 .
.
Pour savoir si elle est génératrice de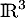 , on peut soit essayer d'exprimer tout vecteur
, on peut soit essayer d'exprimer tout vecteur 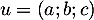 comme combinaison linéaire des vecteurs de la famille
comme combinaison linéaire des vecteurs de la famille 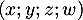 , soit montrer que cette famille de quatre vecteur est de dimension trois donc est forcément génératrice.
On peut prendre par exemple la famille formée les trois premiers vecteurs
, soit montrer que cette famille de quatre vecteur est de dimension trois donc est forcément génératrice.
On peut prendre par exemple la famille formée les trois premiers vecteurs 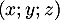 et montrer qu'elle forme une famille libre.
et montrer qu'elle forme une famille libre.
Ainsi,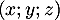 est génératrice de
est génératrice de 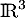 (donc une base) et en y ajoutant un vecteur, on perd la liberté de la famille, mais elle reste encore génératrice.
(donc une base) et en y ajoutant un vecteur, on perd la liberté de la famille, mais elle reste encore génératrice.
Tag:Espace vectoriel
Autres sujets au hasard:

Voir aussi: