Expression d'une série entière avec des fonctions usuelles
Colle de mathématiques
Sujet de colle de maths:- Séries entièresSéries entières
Énoncé du sujet
On considère la série entière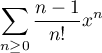 
.
Donner son rayon de convergence et l'exprimer en termes de fonctions usuelles.
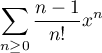. Donner son rayon de convergence et l'exprimer en termes de fonctions usuelles.
Correction
.
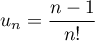On a 
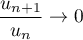et donc le rayon de convergence de la série entière est 
.
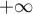Pour déterminer sa somme, on décompose la somme: pour tout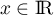
,
![\[\begin{array}{ll}\dsp\sum_{n\geq 0}\frac{n-1}{n!}x^n&=\dsp\sum_{n=1}^{+\infty}\frac{x^n}{(n-1)!}-\sum_{n=0}^{+\infty}\frac{x^n}{n!}\\[.7em]
&\dsp=\sum_{n=0}^{+\infty}\frac{x\cdot x^n}{n!}-e^x=(x-1)e^x\enar\]](/Generateur-Devoirs/Colles/SeriesEnt/exExpSE1_c/5.png)
Correction
Soir.
On a et donc le rayon de convergence de la série entière est .
Pour déterminer sa somme, on décompose la somme: pour tout
,
Tag:Séries entières
Autres sujets au hasard:
Voir aussi: