Étude d'une primitive d'une fonction
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
Énoncé du sujet
Donner une primitive 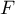 de la fonction
de la fonction 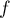 définie par:
définie par:
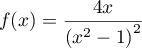 .
.
Donner le sens de variation de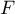 .
.
Donner le sens de variation de
Correction
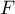 de la fonction
de la fonction 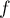 définie par:
définie par:
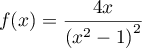 est
est
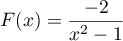 pour
pour 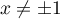 .
.
Comme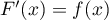 ,
on en déduit que
,
on en déduit que 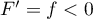 sur
sur ![$]-\infty;-1[\cup]1;+\infty[$](/Generateur-Devoirs/Colles/Calcul/ex3_c/8.png) ,
où
,
où 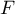 est donc décroissante,
et que
est donc décroissante,
et que 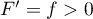 sur
sur ![$]-1;1[$](/Generateur-Devoirs/Colles/Calcul/ex3_c/11.png) où
où 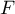 est donc croissante.
est donc croissante.
Correction
Une primitiveComme
Tag:Dérivée
Autres sujets au hasard:

Voir aussi: